時系列分析では、定常性という性質を前提として分析が行われるため、前処理として時系列データを定常過程へ変換する必要があります。
このページでは、時系列データの定常性について解説します。
目次
時系列データにおける定常性とは
時系列データにおける定常性とは、その時系列データの値が時刻 $ t $ に依存しないと見なせることを指します。
定常性をもち、値が確率的に決まる時系列データを定常過程といいます。
たとえば、ホワイトノイズ系列は定常過程です。
ホワイトノイズ系列とは、平均と分散が一定値であり、自己相関を示さず確率的に値が決まるデータです。
自己相関とは、時刻 $ t $ を前後にずらした際に値が元のデータとどれくらい一致するかという性質です。
自己相関が高いと、時系列データの値が周期的に同じような動きをします。
年単位での気温の変化や一日単位での昼夜のサイクルに影響されるような時系列データの場合、自己相関が高くなります。
季節変動をはじめとする自己相関が存在しない時系列データがホワイトノイズ系列です。
定常過程であるホワイトノイズ系列では、周期的な季節変動に加え、トレンドも存在しません。
時間経過とともに一定方向に値が変化していくと平均値が変化していくからです(平均が一定という条件を満たさなくなる)。
注意点としては、循環性はあるがトレンドも季節性(周期的なサイクル)も存在しない時系列データも定常過程です。
周期的な季節変動は予測可能ですが、周期が固定長ではないサイクルでは値が時刻 $ t $ に依存しないと見なせるからです。
定常性は時系列データに様々な手法を適用する際の前提となります。
統計解析や機械学習の手法の多くは、データを同一確率分布から得られた互いに独立な標本の集合とみなしているからです。
トレンドや季節性をもつ非定常な時系列データはこの前提を満たさないため、差分をとるなどの何らかの方法で定常過程に変換する必要があります。
たとえば、時間経過とともに値が増加するトレンドがある2つの時系列データは、本質的には相互に無関係であるにも関わらず、そのまま回帰分析を行うと統計的に有意な強い正の相関があるという結果が出てしまいます。
このような相関を見せかけの回帰(Spurious regression)といいます。
見せかけの回帰は誤った解釈につながるため、あらかじめ定常過程に変換しておくことが重要です。
弱定常性と強定常性
定常性には、制約条件の強さによって弱定常性と強定常性という2種類が存在します。
単に定常性といった場合は弱定常性を表すことが多いです。
時系列データで定常性を確認する目的は、多くの場合、期待値や自己相関などの性質の解析です。
そのため弱定常性の条件で十分であり、制約条件が強くデータから検証困難な場合も多い強定常性を考える必要はありません。
以下では、弱定常性と強定常性の具体的な内容についてふれます。
弱定常性
弱定常性とは、時系列データの平均値、分散、自己共分散の3つが時刻 $ t $ によらず一定である性質を指します。
自己共分散とは、時刻 $ t $ と $ t + h $ ($ h $ は任意の正の数)のときの値の共分散(平均値と値の差(偏差)の積)のことです。
元のデータとラグ $ h $ 分だけずらしたデータがどれくらい類似しているかを表しています。
弱定常性をもつ時系列データは、トレンドや周期的な季節性をもちません。
強定常性
強定常性とは、時系列データの値が全て同一の確率分布をもつ性質を指します。
確率分布が正規分布であれば平均や分散、共分散も時間依存しないため、その時系列データは弱定常性も同時に満たします。
ただし、コーシー分布のように正規分布以外の確率分布をもつ場合は、強定常性を満たしていても弱定常性を満たさないことがあります。
非定常性
データが定常性の条件を満たさない性質を非定常性といいます。
時系列データの非定常性にはトレンド、季節性、分散という3つの要素が存在します。
トレンドとは、平均が時間経過とともに変化することを指します。
トレンドを取り除くためには、直前のデータとの差分をとることで定常化を試みます。
季節性とは、一定の周期をもつ規則的な変動を指します。
言葉通りの季節変化だけではなく、一日の中や一週間単位など直接「季節」とは関係ない循環であっても、一定の周期をもつ場合は季節性です。
季節性を取り除くためには、一定の周期をもつことを利用して季節差分をとることで定常化を試みます。
分散の非定常性とは、データの分散が時間経過とともに変化することを指します。
このような場合、対数変換やBox-Cox変換を行って分散の非定常性(分散の不均一性)を除去することで定常化を試みます。
定常性を調べる方法
時系列データの定常性を調べる方法として、視覚的に確認する方法と統計的検定の2種類の方法があります。
統計的検定の方が厳密ですが、そのような場合であってもまずは可視化を行って視覚的にデータの状態を確認することも重要です。
可視化
データの定常性を確認する際には、まずはじめにデータを可視化します。
明確にトレンドや周期性が見られる場合や異常値などは可視化しただけではっきりわかります。
そのため、統計的検定を行う場合でも最初に可視化をしてデータの分布を見ておくことは重要です。
次の図は、アルファベット(旧グーグル、ティッカー:GOOG)の2017年の日次の株価終値とその前日比差分です。
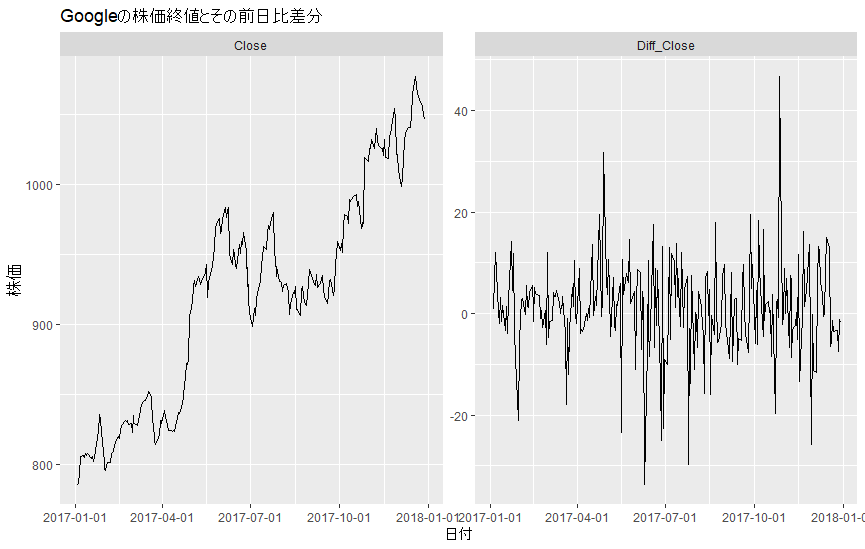
上の図を見ると、左側の株価のグラフは明確に上昇トレンドが確認できるため、明らかに定常過程ではないことがわかります。
そこで、トレンド非定常性を取り除くために、前日終値との差分をとったのが右側のグラフです。
右側のグラフでは、元データで見られた上昇トレンドが取り除かれ、定常過程に近くなりました。
実際に定常化できているかは、統計的検定で確認します。
参考に、上のグラフを作成したRのコードを以下に掲載します。
library(fpp3)
# 特定の年のGoogle(アルファベット)のデータを抽出
y = 2017
goog <- gafa_stock %>%
filter(Symbol == "GOOG", year(Date) == y) %>%
# 株価の前日比差分を取得
mutate(Diff_Close = Close - lag(Close))
# Googleの株価を可視化
goog %>%
select(Date, Close, Diff_Close) %>%
# まとめて描画するために縦持ち変換
pivot_longer(cols = c(Close, Diff_Close), names_to = "Type", values_to = "Value") %>%
ggplot(aes(x = Date, y = Value)) +
geom_line() +
scale_x_date(date_labels = "%Y-%m-%d") +
# 2つにグラフを分ける
facet_wrap(~Type, scales = "free_y") +
labs(x = "日付", y = "株価", title = paste0("Googleの株価終値とその前日比差分(", as.character(y), "年)"))統計的検定(単位根検定)
統計的検定を行うことでデータの定常性を客観的に確認することができます。
データの定常性の確認方法として単位根検定(Unit root test)があります。
単位根過程とは、元の時系列データが非定常かつその差分は定常過程である時系列データです。
単位根過程は1次和分過程(integrated process)または $ I (1) $ 過程とも呼ばれ、$ I $ はARIMAのIに相当します。
単位根検定では、データが単位根過程であること(=非定常であること)を帰無仮説とし、データの定常性を対立仮説としています。
そのため、単位根検定で帰無仮説を棄却できれば、その時系列データの定常性を証明することができます。
以下では、単位根検定の例として、ADF検定とKPSS検定を紹介します。
ADF検定
ADF検定(拡張ディッキー–フラー検定、Augmented Dickey–Fuller test)は、データが単位根過程であること(=非定常であること)を帰無仮説とする単位根検定です。
ADF検定のp値が十分に小さければ、単位根過程であるという帰無仮説が棄却されて定常過程であるという対立仮説が採用されます。
以下にRのtseriesパッケージのadf.test関数を使用してADF検定を行った結果を掲載します。
# ADF検定実施
library(tseries)
# 元データ(上昇トレンドあり)
adf.test(goog$Close, alternative = "stationary", k = 1)
# Augmented Dickey-Fuller Test
#
# data: goog$Close
# Dickey-Fuller = -2.4401, Lag order = 1, p-value = 0.3905
# alternative hypothesis: stationary
# 前日比差分データ
# 欠損を削除してからADF検定
adf.test(na.omit(goog$Diff_Close), alternative = "stationary", k = 1)
# Augmented Dickey-Fuller Test
#
# data: na.omit(goog$Diff_Close)
# Dickey-Fuller = -10.451, Lag order = 1, p-value = 0.01
# alternative hypothesis: stationaryKPSS検定
KPSS検定(Kwiatkowski–Phillips–Schmidt–Shin test)とは、データが定常過程であることを帰無仮説とする単位根検定です。
ADF検定とは帰無仮説が逆であることに注意してください。
KPSS検定のp値が十分に小さければ、定常過程であるという帰無仮説が棄却され、非定常過程であるという対立仮説が採用されます。
そのため、KPSS検定のp値が十分に小さい場合(例:0.05未満)には差分化が必要であることがわかります。
p値が十分に大きい場合には定常過程と見なしてしまいます。
以下に以下にRのfpp3パッケージに含まれるunitroot_kpss関数を使用してKPSS検定を行った結果を掲載します。
# KPSS検定
# 元データ(上昇トレンドあり)
goog %>%
features(Close, unitroot_kpss)
# # A tibble: 1 × 3
# Symbol kpss_stat kpss_pvalue
# <chr> <dbl> <dbl>
# 1 GOOG 3.57 0.01
# 前日比差分データ
goog %>%
features(Diff_Close, unitroot_kpss)
# # A tibble: 1 × 3
# Symbol kpss_stat kpss_pvalue
# <chr> <dbl> <dbl>
# 1 GOOG 0.0447 0.1時系列データの定常化処理
時系列データを定常過程へ変換する処理を定常化処理といいます。
非定常な時系列データの定常性を確認し、定常過程へ変換する方法については、次のページで解説しています。
-

参考時系列データの定常化処理(トレンド・季節性・分散の非定常性の確認と除去)
時系列分析では、定常性という性質を前提として分析が行われるため、前処理として時系列データを定常過程へ変換する必要があります。このページでは、時系列データの定常性を確認し、非定常性を取り除いていく方法に ...
続きを見る
参考文献
時系列データの「定常性」と「3つの非定常性」 株式会社セールスアナリティクス 2024/5/19閲覧
R. J. Hyndman and G. Athanasopoulos, 予測: 原理と実践 (第3版) 2024/5/19閲覧
White Noise Time Series with Python, Machine Learning Mastery 2024/5/19閲覧
曽我部 東馬 「Pythonによる異常検知」オーム社 (2021)
定常性の定義(弱定常性および強定常性) このめのエコノミ 2024/5/21閲覧
沖本 竜義「経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)」 朝倉書店(2010)
Unit root test, Wikipedia 2024/5/19閲覧
時系列分析の単位根過程、和分過程、ランダムウォークを解説 株式会社AVILEN 2024/5/19閲覧