データ数が少ないスモールデータに適用できる統計学的検定の手法として、Brunner-Munzel検定(ブルンナー=ムンツェル検定)と並べ替え検定があります。
ここでは、標本サイズが小さいデータに対して二群比較に使われる検定手法と比較しながら、これらの検定手法について紹介します。
二群比較の検定手法と前提条件
二群比較の検定手法の中には、標本分布の正規性や等分散性を仮定するものがあります。
標本サイズが小さいスモールデータでは、正規性や等分散性を仮定できない場合も多く、正規性や等分散性を仮定する検定手法を使うと適切な結論を導くことができません。
そのため、検定手法ごとの「仮定」を把握して使い分ける必要があります。
正規性と等分散性の仮定を要するか否かは次のとおりです。
表 二群比較の検定手法における正規性と等分散性の仮定
| 検定手法 | 正規性仮定 | 等分散性仮定 |
| Student' s t-test(スチューデントのt検定) | Yes | Yes |
| Welch's t-test(ウェルチのt検定) | Yes | No |
| Mann-Whitney U test(マンホイットニーのU検定) | No | Yes |
| Brunner-Munzel test(ブルンナー=ムンツェル検定) | No | No |
上表より、正規性を仮定できる場合はウェルチのt検定を使い、仮定できない場合はマンホイットニーのU検定(ウィルコクソンの順位和検定)を使えばよいことがわかります。
しかし、マンホイットニーのU検定は等分散性の仮定を必要とするため、等分散性を仮定できない場合は利用できません。
そこで、正規性や等分散性を仮定せずに使用できる検定手法として、Brunner-Munzel検定を紹介します。
Brunner-Munzel検定の統計量に対して並べ替え検定を行う並べ替えBrunner-Munzel検定は、単独のBrunner-Munzel検定よりも正確に計算できます。
以下では、並べ替え検定とBrunner-Munzel検定について紹介します。
並べ替え検定(Permutation test)
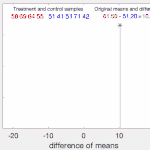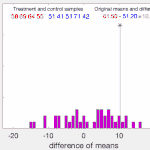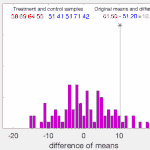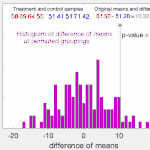
並べ替えの検定は、リサンプリングしたデータと元のデータの統計量を検定する手法です。
検定手法というよりもリサンプリングの一種として扱われ、標本サイズが小さいデータに対して使われます。
詳細については、次のページで解説しています。
-

参考並べ替え検定
データ数が少ない(標本サイズが小さい)スモールデータに適用できる統計学的検定の手法として並べ替え検定があります。 ここでは、並べ替え検定の手順について紹介します。 他の二群比較の検定手法との比較やRで ...
続きを見る
Brunner-Munzel検定
Brunner-Munzel検定は、対応のない二標本の分布の同一性を検定する方法です。
「群Aと群Bから値を1つずつ取り出したとき、群Aの値が大きい確率と群Bの値が大きい確率が等しい」という帰無仮説を検定します。
正規性や等分散性を仮定せずに使用できます。
マンホイットニーのU検定とは異なり、等分散性を仮定せずに使用できるというメリットがあります。
そのため、スモールデータに対する検定手法として便利です。
Brunner-Munzel検定の統計量に対して並べ替え検定を行う並べ替えBrunner-Munzel検定を行うことで、より正確なp値を算出できます。
Rによる実装
ここからは、Rで二群比較の検定手法の実装について紹介します。
今回は、標本X (n=10, sd=3.0)と標本Y (n=8, sd=1.2) の二標本の差の検定を行います。
データは以下のように、標準正規分布に従う乱数を生成して標本としました。
# Rで二群比較の検定を実施
rm(list = ls())
# ライブラリの読み込み --------------------------------------------------------------
# install.packages("exactRankTests",dependencies = TRUE)
library(exactRankTests)
# データ ----------------------------------------------------------------
# 標本サイズ
n1 = 10
n2 = 8
# 標準偏差
sigma1 = 3.0
sigma2 = 1.2
x <- rnorm(n1, mean = 10, sd = sigma1)
y <- rnorm(n2, mean = 9, sd = sigma2)
# > x
# [1] 11.547135 7.147759 8.582447 9.725163 9.664775 16.035391 14.213797
# [8] 8.210826 12.632474 9.008821
# > y
# [1] 9.094034 8.543365 8.167008 7.138753 8.407430 11.198398 7.399952
# [8] 10.058556はじめに、二標本の等分散性と正規性を確認します。
等分散性の確認にはF検定、正規性の確認にはコルモゴロフ=スミルノフ検定(Kolmogorov-Smirnov test, KS test)を使用しています。
データセットの作成方法より、等分散性は成立せず、正規性は成立することが期待されます(ただし、正規性は標本サイズが小さいと成立しない)。
# 検定実施 --------------------------------------------------------------
# 等分散性・正規性確認用
# F test(等分散性の検定)
var.test(x, y)$p.value
# [1] 0.008092068
# Kolmogorov-Smirnov test(正規性の検定)
ks.test(x = x, y = "pnorm", alternative = "two.sided", exact = TRUE)$p.value
# [1] 0
ks.test(x = y, y = "pnorm", alternative = "two.sided", exact = TRUE)$p.value
# [1] 0検定結果より、二標本間には等分散性は成立せず、正規性は成立していることがわかりました。
このような標本に対しては、等分散性の仮定が不要なウェルチのt検定やBrunner-Munzel検定が適切です。
今回は正規性を仮定できましたが、標本サイズが小さい場合には正規性を仮定できない場合も多いので、多重検定を回避する観点からもBrunner-Munzel検定を選択するのがよいと思われます。
以下のコードでは、5パターンの検定を実施してp値を算出しています。
帰無仮説は二群間に差がないことです。
# 以下、二群比較の検定実施
# 1. Permutation Test(並べ替え検定)
perm.test(x, y, alternative = "greater", paired = FALSE, exact = TRUE)$p.value
# [1] 0.0840075
# 2. Exact Wilcoxon rank sum test(マンホイットニーのU検定)
wilcox.exact(x, y, alternative = "greater", paired = FALSE, exact = TRUE)$p.value
# [1] 0.03379953
# 3. Student's t-test
t.test(x, y, alternative = "greater", var.equal = TRUE, paired = FALSE)$p.value
# [1] 0.06419339
# 3. Welch's t-test
t.test(x, y, alternative = "greater", var.equal = FALSE, paired = FALSE)$p.value
# [1] 0.05242814
# 4. Brunner-Munzel test
brunnermunzel.test(x, y, alternative = "greater", perm = FALSE)$p.value
# [1] 0.02773275
# 5. Permuted Brunner-Munzel Test(並べ替えBrunner-Munzel検定)
brunnermunzel.permutation.test(x, y, alternative = "greater")$p.value
# [1] 0.02975456検定結果を見ると、4番目のBrunner-Munzel検定と5番目の並べ替えBrunner-Munzel検定のみp値が0.05を下回り、帰無仮説を棄却できています。
今回のデータは母平均の差に対して標準偏差が大きい分布でしたが、Brunner-Munzel検定を使うことで差があることを示すことができました。
もちろん、データセット次第で検定結果は変わってきます。
こちらのサイトで詳しく検討されていますが、スモールデータに対する中央値の検定手法としてはBrunner-Munzel検定を第一選択として良いように思います。
参考文献
マイナーだけど最強の統計的検定 Brunner-Munzel 検定 ほくそ笑む R言語と統計解析について 2023/5/6閲覧
Brunner-Munzel検定 三重大学教育学部奥村研究室 2023/5/6閲覧
ブルンナー=ムンツェル検定 BellCurve 株式会社社会情報サービス 2023/5/6閲覧
Peter Bruce et al.「データサイエンスのための統計学入門 第2版」 オライリージャパン (2020)
水本 篤「サンプルサイズが小さい場合の統計的検定の比較」統計数理研究所共同研究リポート 238 1-14 (2010)
Mann-Whitney U 検定と並べ替え検定:小標本の正確検定 生物科学研究所 井口研究室 2023/5/5閲覧
Mann–Whitney U test, Wikipedia 2023/5/6閲覧