ここでは、独立した２つのグループの分布に差があるかを比較する統計的検定を行う際の手法選択の流れと注意点についてまとめます。
検定手法として有名なのはｔ検定ですが、正規性などの仮定が成り立つ場合にしか使用することができません。
さらに、多重検定を行ってはいけないなどの注意点もあります。
このような注意点にふれながら手法選択の流れを見ていきます。
目次
手法選択の流れ
独立した二群比較の検定手法選択の流れ。はじめに二群間にデータの対応があるかで検定手法が分かれる。次に分布の正規性の有無によって、パラメトリック/ノンパラメトリックの検定手法を採用する。
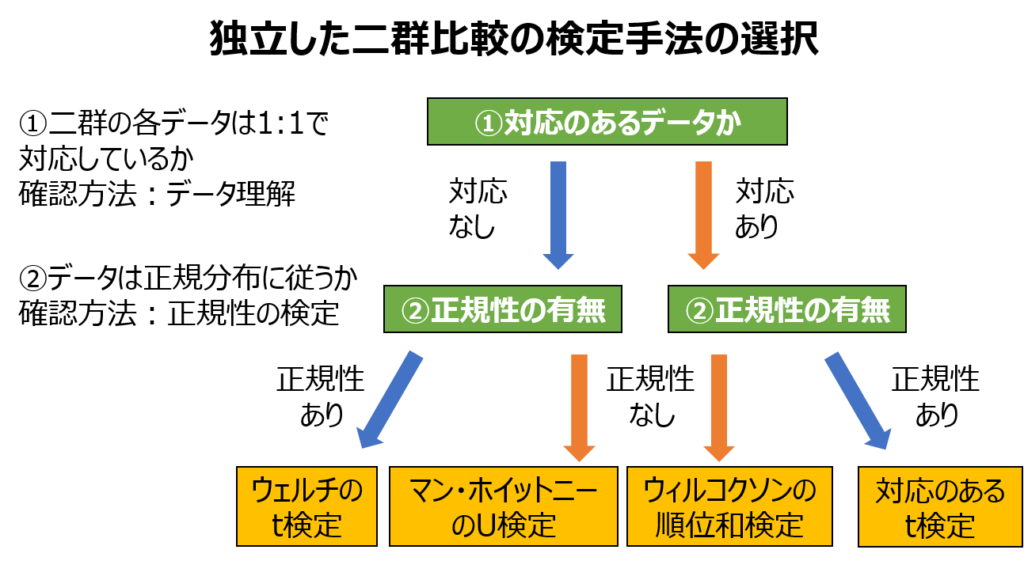
上図は、手法選択の流れをまとめたものです。
はじめに比較したい２つの群のデータの間に対応があるかを判断します。
次に、正規性の有無を確認した上で、パラメトリック（分布の正規性を仮定）あるいはノンパラメトリック（特定の分布を前提としない）の検定手法を採用します。
検定を行う際には多重検定にならないように注意する必要があります。
以下の項目で順番に説明します。
二群間のデータの対応の有無
はじめに２つの群のデータの対応の有無を確認します。
２つの群に「対応がある」とは、２つの群の各データが１：１でペアを作れることです。
たとえば、A駅とB駅の売上の季節変動に差があるかを比較するために、３年間の毎月の両駅の売上データを用意したとします。
このデータはA駅もB駅も１年目の１ヶ月目のデータが１つずつ存在し、１：１で対応づけることができます。
他の月も同様になっており、A駅しかデータが無いような場合はその月のB駅のデータが欠損しているとみなされます。
このような二群（A駅とB駅）は、対応のあるデータです。
一方、男女各500人の月間利用金額のデータを用意して男性と女性の月間利用金額を比較する場合は、対応がないデータとなります。
サンプルサイズ（データの数）は男性も女性も同じですが、500人の男性と女性は１：１で対応づけることができません。
このような二群（男性と女性）は、対応のないデータです。
以上のように二群間のデータの対応の有無を判断した上で、正規性の有無を確認します。
正規性の有無
次にデータの分布に正規性を仮定できるかを確認します。
分布の正規性を仮定できる場合はパラメトリック（分布の正規性を仮定）、仮定できない場合はノンパラメトリック（特定の分布を前提としない）の検定手法を採用します。
正規性の確認方法には次のような方法があります。
・ヒストグラムを描く
・Q-Qプロットを描く
・正規性の検定（コルモゴロフ=スミルノフ検定やシャピロ=ウィルク検定）
以下の項目で順番に説明します。
ヒストグラムを描く
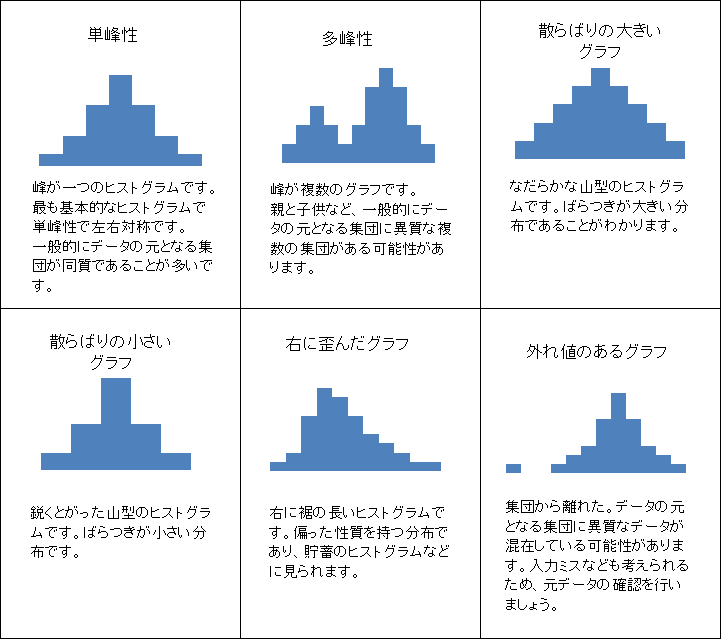
様々な分布のヒストグラム。出典：ヒストグラム なるほど統計学園 総務省統計局 2022/12/29閲覧
最も簡単な方法はヒストグラムを描いてみることです。
単純で厳密性に欠く方法ですが、あなどれません。
正規性を仮定できないデータにｔ検定を行ったことで問題がおきている場合には、上図の「多峰性」や「右に歪んだグラフ」のように正規分布から極端に乖離した分布になっていることがしばしばあります。
Q-Qプロットを描く
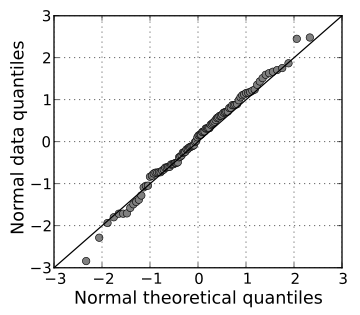
ランダムに生成された独立した標準正規分布のデータをプロットしたQ-Qプロット。横軸は理論的な確率分布の分位数、縦軸に実際のデータの分位数である。データのプロットが直線状に並ぶため正規性を仮定できると判断する。出典：Wikimedia Commons, ©Skbkekas, CC BY-SA 3.0, 2022/12/29閲覧
２つ目の確認方法はQ-Qプロット（Q-Q plot, quantile-quantile plot）を描くことです。
Q-Qプロットとは、理論的なデータの分布と実際のデータの分布がどの程度一致するか視覚的に確認するために作成するグラフのことです。
上図のように、横軸に理論的な分布（今回は正規分布）、縦軸に実際のデータの分布をとってプロットします。
実際のデータが正規分布に従う場合は、上図のように直線状にプロットが並びます。
このようにプロットが直線からどの程度乖離するかを視覚的に確認することで、データの正規性を判断します。
視覚的な確認方法ですが、後述する多重検定を回避するためにあえて正規性の検定を行わず、Q-Qプロットでの確認が行われる場合があります。
正規性の検定
３つ目の確認方法は正規性の検定です。
先程のQ-Qプロットで対角線からプロットがどの程度離れているかが検定統計量になります。
正規性の検定には、コルモゴロフ=スミルノフ検定（KS検定, Kolmogorov–Smirnov test）やシャピロ=ウィルク検定（SW検定, Shapiro–Wilk test）があります。
これらの検定の帰無仮説は「データの分布が特定の分布（今回は正規分布）に従っている」というものです。
そのため、帰無仮説が棄却された場合は、データの分布が正規分布ではないことになります。
一方、帰無仮説が棄却されない場合は、厳密には「正規分布ではないとは言えない」となりますが、明確に正規分布とは異なる分布だと断定できないため、近似的に正規分布と見なせると考えます。
そのため、帰無仮説が棄却されない場合は正規分布とみなして検定手法を選択します。
KS検定とSW検定の使い分けのポイントはデータ数の大小です。
KS検定ははおおむね数千程度以上のサンプルサイズ（データ数）に対してSW検定より良い結果を与えるとされています。
一方、SW検定はおおむね50程度の少ないサンプルサイズに対して適しています。
使い分けの目安としては、おおむね2000以下のサンプルサイズに対してはSW検定を使い、それ以上の場合はKS検定を使います。
多重検定の回避
検定を複数回組み合わせて行うと、個々の検定結果が正確であっても、それらを組み合わせた全体では有意水準がずれてしまうという問題があります（多重検定）。
このような多重検定は、検定結果の解釈を間違える原因になるため、可能な限り回避するのが望ましいです。
ここでは、検定手法の選択において多重検定に対する対処不法を３通り紹介します。
多重検定になる場面とその対処方法は次のとおりです。
１．正規性の検定（二群それぞれに対して実施しない）
→正規性の検定は二群に対して一括で実施
２．検定手法選択のために正規性の検定を実施
→検定手法選択のための正規性の確認は検定以外で
３．検定手法選択のために等分散性の検定
→等分散性を前提としない手法を選択
詳細について順に説明します。
正規性の検定は二群に対して一括で実施
正規性の検定は検定したい二群に対して個別に行うのではなく、各群それぞれに対して中心化を行い、二群のデータをまとめて使用して検定を行います。
独立した２つの正規分布の和もまた正規分布になるため、二群のデータをまとめる操作ができます。
中心化とは、各データの値を平均値からの差（残差）に変換する操作です。
ちなみに、中心化した値をさらに標準偏差で割った場合は標準化といいます。
中心化を行うことで、分布の位置が異なる二群についても二群をまとめることができます。
中心化だけを行った値を使用することで、二群のデータの分布のみをまとめて比較することができます。
中心化した値を使って検定を一回で行う理由は主に２つあります。
１つは多重検定の回避です。
群ごとに正規性の検定を行うと多重検定となり、二群まとめて見たときに有意水準がずれます。
１回の検定単独では、検定結果の有意水準は定めた通りです（有意水準0.05なら0.05）。
しかし、二つの群それぞれについて正規性を仮定できるかを考えた場合、どちらか片方の群で第一種過誤（偽陽性、正規性を仮定できるにも関わらず棄却）がおきると、もう一方の群で第一種過誤がおきなくても、最終的な判断の誤りに繋がります。
このため、第一種過誤（偽陽性）がおきる確率は単独の検定よりも大きくなり（有意水準0.05なら全体で0.10）、本来の有意水準から外れます。
これを回避するためには、中心化した値を使用して検定を一回にします。
２つ目の理由として、二群の検定結果が異なる場合があることです。
片方の群で正規性を仮定できるが、もう片方の群で正規性を仮定できないような二群を比較する際には、ｔ検定を適用できるか扱いに困ります。
このような悩みは、一括で検定を行うことで回避することができます。
検定手法選択のための正規性の確認は検定以外で
検定手法選択のために正規性を確認する場合、正規性の検定を行うと多重検定になります。
多重検定を回避するためには、そもそも正規性の検定を行わないで正規性を確認するという考え方があります。
検定以外の手法で正規性を確認するアプローチとしては、ヒストグラムを書いたり、Q-Qプロットから正規性を確認するといった方法があります。
等分散性を前提としない手法を選択
平均値の差のｔ検定では、等分散性の検定を行い、等分散性を仮定できるなら通常のｔ検定、仮定できないならばウェルチのｔ検定（Welch's t test）を使用するとされています。
しかし、この方法では多重検定になってしまいます。
多重検定を回避するという観点から、はじめからウェルチの検定を行う考え方があります。
上のフローチャートでも、対応のない正規性を仮定できるデータに関しては、ウェルチのｔ検定を適用する形で作成しています。
参考文献
マン・ホイットニーのU検定（概要とpython実装） データ分析とケモインフォe try 2022/12/28閲覧
スプレッドシートで行うMann-WhitneyのU検定 Fractal Prologue 2022/12/28閲覧
32-2. 正規性の確認 統計WEB 株式会社 社会情報サービス 2022/12/29閲覧
Q-Qプロット ウィキペディア 2022/12/29閲覧
データ解析 第八回「検定」 Taiji Suzuki's home page 2022/12/29閲覧
正規性の検定 井出草平の研究ノート 2022/12/29閲覧
Sarah Boslaugh 「統計クイックリファレンス 第2版」 オライリージャパン (2015)
４章 母集団と指定値との量的データの検定 福山平成大学 2022/12/29閲覧
Kolmogorov-SmirnovとShapiro-Wilkの違い IBM 2022/12/29閲覧
正規性の検定の選択と結果の解釈 OriginLab 2022/12/29閲覧
等分散検定から t検定，ウェルチ検定，U検定への問題点 生物科学研究所 井口研究室 2023/1/9閲覧
t 検定の正規性も残差を調べる：検定の多重性問題 生物科学研究所 井口研究室 2023/1/9閲覧