このページでは、時系列データの特徴把握を行います。
具体的には、可視化(ACF, PACFの確認)や季節分解を行ってデータの特徴把握をした上で、単位根検定を実施します。
時系列データの特徴把握
このページでは、米国の月間航空機搭乗者数のサンプルデータを使って時系列データの特徴把握を行います。
以下では、サンプルデータについてふれたうえで、可視化による特徴把握・自己相関の確認、seasonal_decompose関数による季節分解を行っていきます。
データについて
データセットはKaggleのAirPassangersを使用しました。
これは、1949-1960年の米国の旅客機の月間搭乗者数のデータ(Air Passangers)です。
データとしては、年月と搭乗者数の2つのカラムだけのシンプルなものです。
なお、過去に同じデータを使ってprophetでモデル化した際の結果についてはこちらを参照して下さい。
可視化・相関確認
はじめに、データを可視化して特徴を把握します。
データを読み込み、前処理として前月比変化(%単位)を算出し、乗客数実数と前月比のそれぞれについて時系列推移を確認します。
次の図は、元データ(左列)と前月比差分(右側)を可視化した結果です。
上段は元データの時系列推移、中段と下段はそれぞれ自己相関係数(ACF)、偏自己相関係数(PACF)を示したものです。
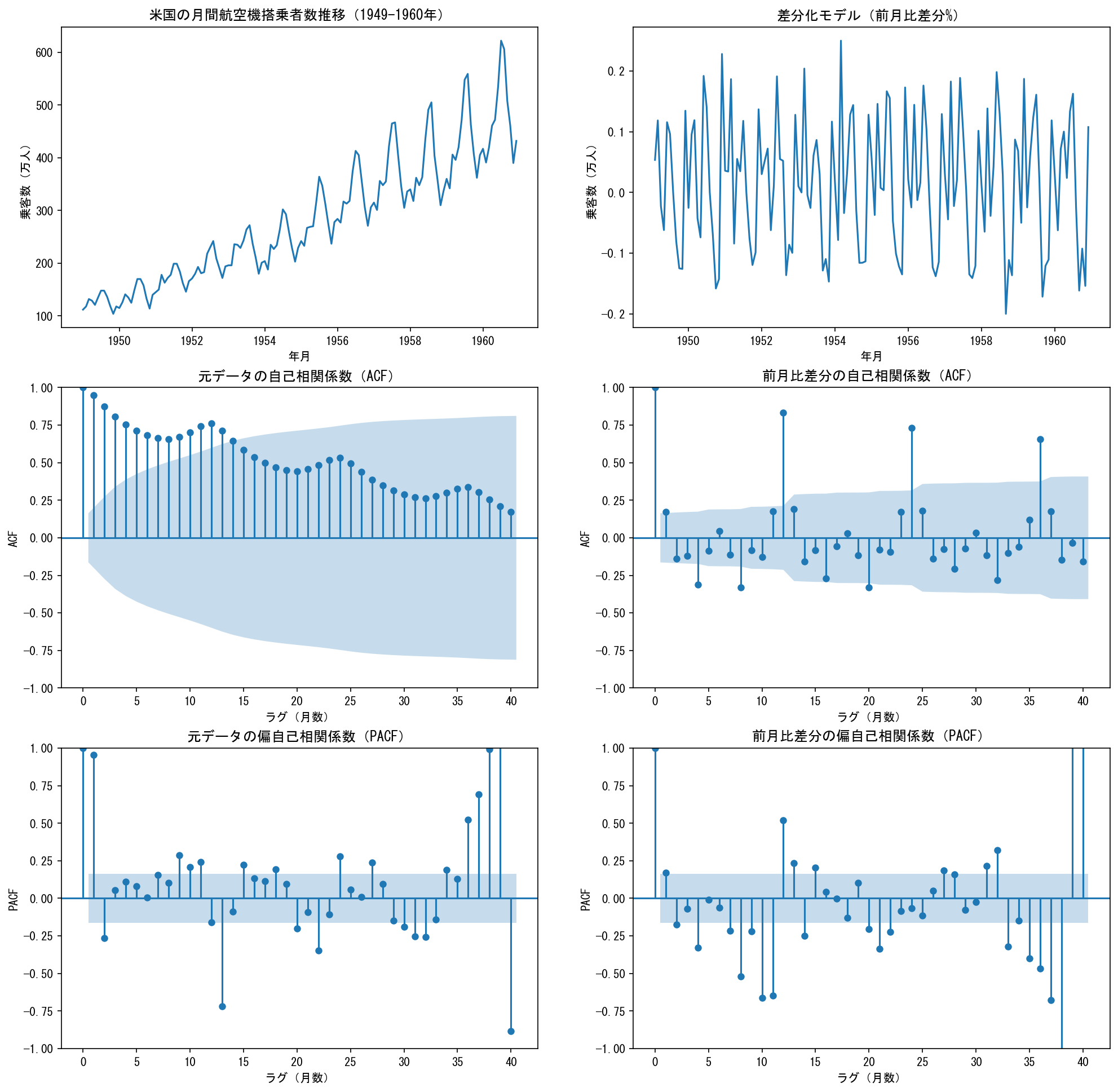
上段を見ると、乗客数は期間中には上昇トレンドですが、周期的に乗客数がサイクルしながら増えていることがわかります。
この上昇トレンド中のサイクルの周期を確かめたのが中段です。
中段では、自己相関係数(ACF, AutoCorrelation Function)を指標として「ある地点のデータは何ヶ月後のデータと相関が高いか」を調べています。
元データは定常過程ではないので前月比差分データのACFを見ます。
前月比差分のACF値を見ると、大部分は95%信頼区間(水色で塗りつぶした領域)に含まれ、有意な自己相関は見られません。
しかし、12, 24 ,36か月のラグをとった場合は信頼区間から外れるほどACFが高くなります。
これは、航空機搭乗者数が1年周期の季節成分をもつデータであることを示しています。
最後に、偏自己相関係数(PACF, Partial AutoCorrelation Function)についても確認します。
ACFだけではなくPACFも確認するのは、偽相関の影響を取り除いた場合にどうなるかを確かめるためです。
前月比差分のACFでは12, 24, 36か月のラグでACF値が高くなっていました。
しかし、PACFでは12か月のみが正のPACF値を取り、24, 36ヶ月では正の自己相関の特徴が無くなっています。
以上の結果より、12か月周期(=1年周期)で季節性があるデータであることが確かめられました。
ここまでの処理のコードは以下のとおりです。
<前処理部分>
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
plt.rcParams['font.family'] = 'MS Gothic'
# データの読み込み
file_path = '../00_data/01_kaggle_Air_Passengers/AirPassengers.csv'
df = pd.read_csv(file_path)
# カラム名変更
df = df.rename(columns={'#Passengers':'乗客数'})
# 年月データを型変換
df['Month'] = pd.DatetimeIndex(df['Month'])
# 差分取得(前月比±何%といった形式で算出)
df['前月比%'] = df['乗客数']/df['乗客数'].shift(1) -1
# 年月をインデックスへ
index_cols = ['Month']
df = df.set_index(index_cols)
# 元データから可視化用に必要箇所取得
# 乗客数
use_cols = ['乗客数']
df_rawdata = df[use_cols]
display(df_rawdata.head(2))
# 前月比%
use_cols = ['前月比%']
df_zengetsuhi = df[use_cols]
# 前月比を算出できない月は削除
df_zengetsuhi = df_zengetsuhi[df_zengetsuhi['前月比%'].notnull()]
display(df_zengetsuhi.head(2))<可視化>
# 可視化
fig, axes = plt.subplots(3, 2, figsize=(16, 16))
# 元データ分析の可視化
axes[0][0].plot(df_rawdata)
axes[0][0].set_title("米国の月間航空機搭乗者数推移(1949-1960年)")
axes[0][0].set_xlabel("年月")
axes[0][0].set_ylabel("乗客数(万人)")
fig = sm.graphics.tsa.plot_acf(df_rawdata, lags=40, ax=axes[1][0])
axes[1][0].set_title("元データの自己相関係数(ACF)")
axes[1][0].set_xlabel("ラグ(月数)")
axes[1][0].set_ylabel("ACF")
fig = sm.graphics.tsa.plot_pacf(df_rawdata, lags=40, ax=axes[2][0])
axes[2][0].set_title("元データの偏自己相関係数(PACF)")
axes[2][0].set_xlabel("ラグ(月数)")
axes[2][0].set_ylabel("PACF")
# 差分化モデルの可視化
axes[0][1].plot(df_zengetsuhi.dropna(), alpha=1)
axes[0][1].set_title("差分化モデル(前月比差分%)")
axes[0][1].set_xlabel("年月")
axes[0][1].set_ylabel("乗客数(万人)")
fig = sm.graphics.tsa.plot_acf(df_zengetsuhi, lags=40, ax=axes[1][1])
axes[1][1].set_title("前月比差分の自己相関係数(ACF)")
axes[1][1].set_xlabel("ラグ(月数)")
axes[1][1].set_ylabel("ACF")
fig = sm.graphics.tsa.plot_pacf(df_zengetsuhi, lags=40, ax=axes[2][1])
axes[2][1].set_title("前月比差分の偏自己相関係数(PACF)")
axes[2][1].set_xlabel("ラグ(月数)")
axes[2][1].set_ylabel("PACF")
# 画像出力
out_path = '../02_work/03_時系列予測_ARIMA/01_可視化/01_可視化_搭乗者数推移_ACF_PAXF_前月比差分.png'
fig.savefig(out_path, dpi=150, bbox_inches='tight')季節分解
次に季節分解を行います。
先程のACFとPACFの結果より季節性は12か月周期のサイクルであると考えられるため、周期12ヶ月で季節分解を行います。
次の図は、statsmodels.tsa.seasonal_decompose関数を使って季節分解を行って元データと分解後の各成分の推移を可視化したものです。
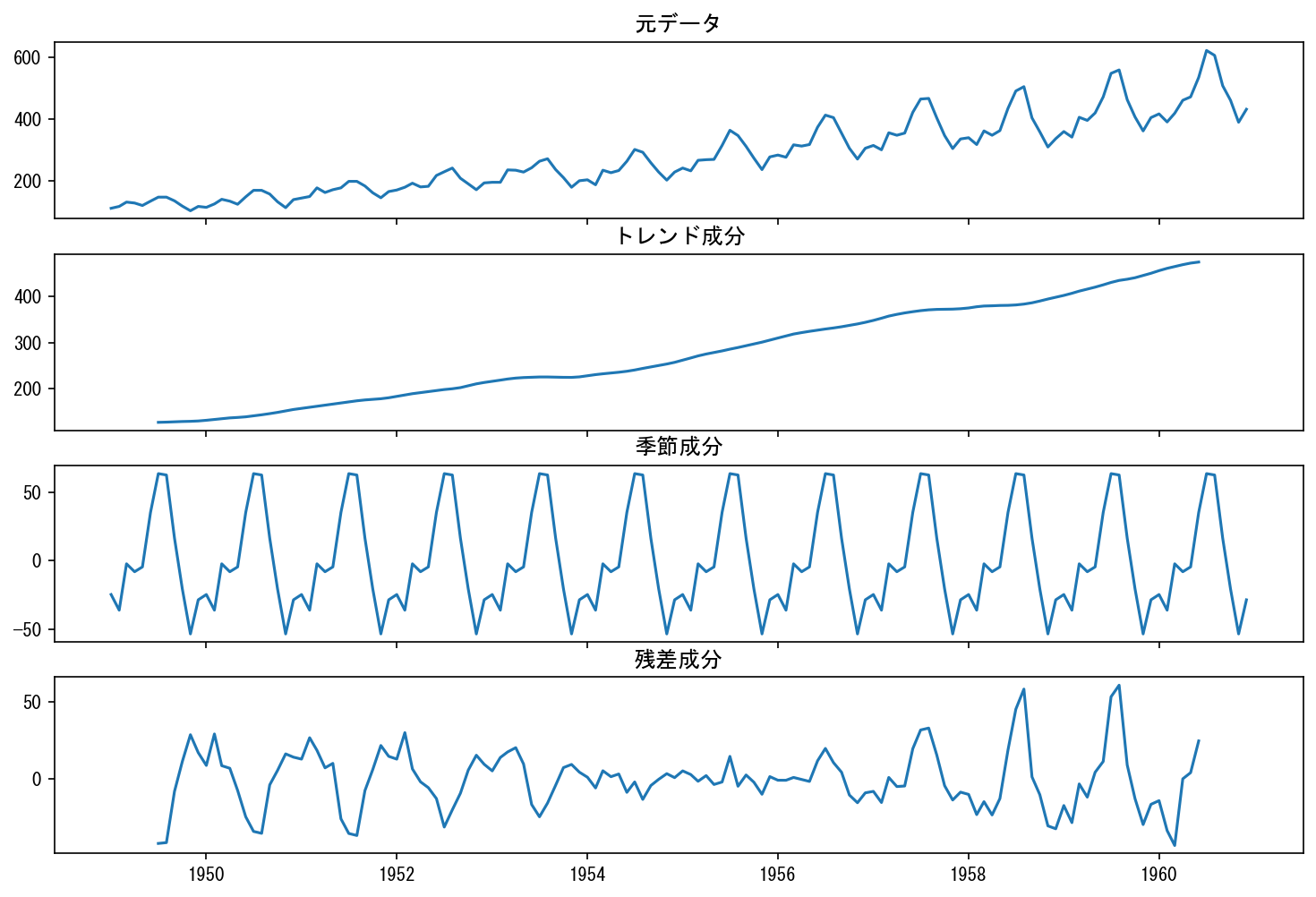
周期12ヶ月で季節分解を行った結果、トレンド成分は上昇トレンドが明確に見られ、季節成分からは周期的な変動が見られます(毎年7-8月頃がピークで11月頃が底)。
トレンド成分や残差成分には循環的な変動は見られないため、このデータの周期的な変動は12ヶ月周期の季節変動だけで説明できそうです。
以上より、このデータは単位根仮定であり、さらなる差分化は必要無さそうです。
単位根検定は次の項目で実施します。
最後に、コードを掲載します。
# 成分分解
# コレログラムでの結果をふまえて季節周期は12か月として成分分解
period = 12
dcmp = sm.tsa.seasonal_decompose(df_rawdata, model='additive', period=period)
# 可視化
# 元データ、トレンド成分、季節成分、残差(不規則変動)の順に縦に並べて可視化
titles = ['元データ', 'トレンド成分', '季節成分', '残差成分']
datas = [dcmp.observed, dcmp.trend, dcmp.seasonal, dcmp.resid]
fig, axes = plt.subplots(4, 1, figsize=(12, 8), sharex=True)
for i, data in enumerate(datas):
axes[i].set_title(titles[i])
axes[i].plot(data)
# 画像出力
out_path = '../02_work/03_時系列予測_ARIMA/01_可視化/01_可視化_搭乗者数推移_季節分解.png'
fig.savefig(out_path, dpi=150, bbox_inches='tight')
plt.show()単位根検定
ここまでの可視化の結果から元データは単位根仮定であることが想定されるので、単位根検定の一種であるADF検定を行って実際に確かめてみます。
ADF検定では、データが単位根過程であること(=非定常だが差分化すると定常過程である)が帰無仮説です。
そのため、検定で帰無仮説を棄却できなかったとしても、「単位根仮定ではないとは言えない」であって厳密には単位根仮定であることを証明したことになはなりませんが、ここでは簡便のためにADF検定で単位根検定を行います。
以下のコードでは、元データだけではなく、比較用に差分化後のデータでもADF検定を行った結果です。
# 単位根検定(ADF検定)実施
# 元データ
adf_rawdata = sm.tsa.stattools.adfuller(df_rawdata)
print('ADF検定結果(元データ):', adf_rawdata)
# 差分化後データ
adf_zengetsuhi = sm.tsa.stattools.adfuller(df_zengetsuhi)
print('ADF検定結果(差分化データ):', adf_zengetsuhi)
# adfullerの出力は順に、テスト統計値、p値、ラグ数、使用したデータ数、検定統計量の臨界値(1%,5%,10%水準)、AIC
# ADF検定結果(元データ): (0.8153688792060597, 0.9918802434376411, 13, 130, {'1%': -3.4816817173418295, '5%': -2.8840418343195267, '10%': -2.578770059171598}, 996.692930839019)
# ADF検定結果(差分化データ): (-2.926108907545377, 0.04239503972524038, 14, 128, {'1%': -3.4825006939887997, '5%': -2.884397984161377, '10%': -2.578960197753906}, -425.9255544019345)元データでADF検定を行った場合のp値は0.99なので帰無仮説を棄却できず、単位根検定であると考えられます(厳密には、単位根仮定ではないとは言えない)。
一方、差分化後のデータの場合はp値が0.04となり有意水準5%で帰無仮説を棄却できるため、単位根仮定ではないと言えます。
以上の結果から、元データは非定常であるが差分化すると定常過程になる単位根過程であると考えられます。
参考文献
PythonでのARIMAモデルを使った時系列データの予測の基礎[後編] ブレインズテクノロジー株式会社 2024/6/23閲覧
R. J. Hyndman and G. Athanasopoulos, 予測: 原理と実践 (第3版) 2024/6/23閲覧
Pythonで時系列解析・超入門(その1)時系列データに対する3つの特徴把握方法 株式会社セールスアナリティクス 2024/6/23閲覧
時系列解析の自己相関係数と偏自己相関係数、相互相関係数を分かりやすく解説 Data Driven Knowledgebase 2024/6/23閲覧
Python: statsmodels で時系列データを基本成分に分解する CUBE SUGAR CONTAINER 2024/6/23閲覧
時系列分析 その5 ARIMA、単位根過程 Qiita 2024/6/29閲覧