データ数が少ない(標本サイズが小さい)スモールデータに適用できる統計学的検定の手法として並べ替え検定があります。
ここでは、並べ替え検定の手順について紹介します。
他の二群比較の検定手法との比較やRでの実装についてはこちらで紹介します。
並べ替え検定(Permutation test)とは
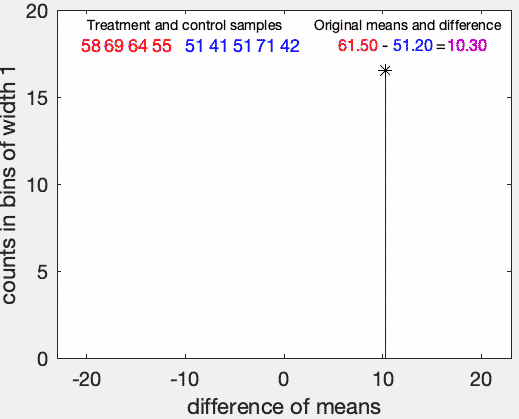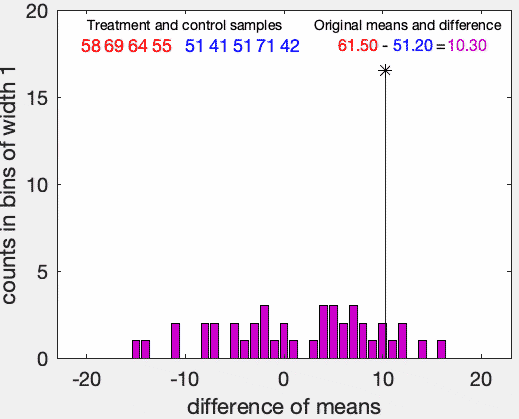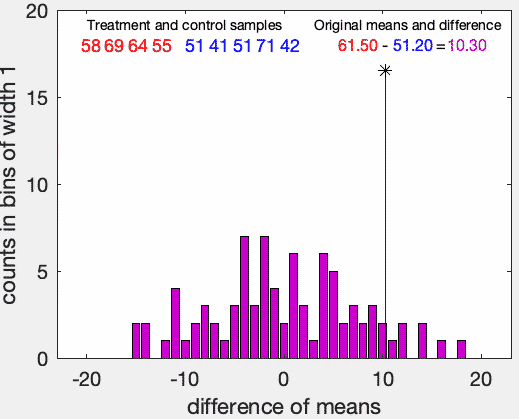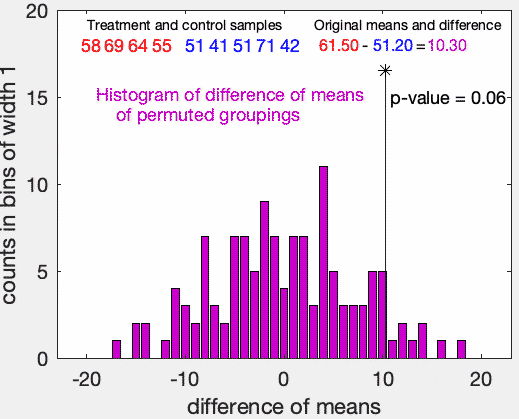
並べ替え検定の例。赤の群(n=4)の方が青の群(n=5)よりも大きいかを検定にしている。帰無仮説は赤の群の方と青の群の分布が同じことである。仮説の p 値は、リサンプリングした際に元のサンプルの平均の差と同じかそれ以上の差を与える割合として推定される。この例では、帰無仮説はp = 0.05の水準で棄却できない。出典:Wikimedia Commons, ©Dicklyon, CC BY-SA 4.0, 2023/5/5閲覧
並べ替え検定は、リサンプリングしたデータと元のデータの統計量を検定する手法です。
リサンプリングの一種として扱われ、標本サイズが小さいデータに対して使われます。
リサンプリングとは、データセットから無作為抽出を繰り返して新しい標本を大量に作り出す方法です。
データ数が少なく(=標本サイズが小さく)正規分布を仮定できない場合に使用するノンパラメトリックな検定手法の一種です。
たとえば、データ数が少なく正規性を仮定できずにt検定を使えない場合、並べ替え検定により差の検定を実施できます。
具体例と手順は次の項目のようになります。
並べ替え検定の具体例・手順
<例>
群A (n=7) の平均値の方が群B (n=6) の平均値よりも大きいことを統計的に確かめたい
<データセット>
群A:52, 50, 55, 48, 47, 50, 51
群B:51, 48, 45, 50, 45, 46
<帰無仮説>
帰無仮説:群Aの平均値と群Bの平均値の差はゼロである
<手順>
1.群Aと群Bの平均値の差を算出(2.93)
2.群Aと群Bのデータを一緒にまとめ、1つのデータセットABを作成
3.データセットABから非復元無作為抽出を行い、群Aと同じサイズの標本A1 (n=7)を抽出(リサンプリング)
※抽出した標本は標本サイズが群Aと同じだけで、無作為抽出なので他グループのデータが含有
4.残りのデータから非復元無作為抽出を行い、群Bと同じサイズの標本B1 (n=6)を抽出
5.標本A1, B1から検定を行うために必要な統計量や推定値(今回はA1 - B1)を計算
6.上記3~5をn回繰り返して統計量の分布(A1 - B1, A2 - B2, …, An - Bn)を確認
7.上記6の統計量Ai- Bi の分布において0未満になるものが何%存在するか(p値)を確認し、有意水準以下であれば帰無仮説を棄却
※統計量の分布は中心極限定理により元のデータセットの分布に関わらずn数を増やすことで正規分布に収束
ポイント
並べ替え検定の注意点としては、標本が母集団を代表している必要があるという点です。
少数の標本から多数のデータをリサンプリングするため、標本が母集団を代表するような分布になっていない場合は並べ替え検定の結果は母集団を表すものにはなりません。
特に標本サイズが極端に小さい場合、母集団を必ずしも適切に表しているとは限りません。
並べ替え検定の実装
並べ替え検定の実装は、RのexactRankTestsパッケージのperm.test関数が便利です。
Rでの実装についてはこちらで紹介しています。
参考文献
Peter Bruce et al.「データサイエンスのための統計学入門 第2版」 オライリージャパン (2020)
水本 篤「サンプルサイズが小さい場合の統計的検定の比較」統計数理研究所共同研究リポート 238 1-14 (2010)
中心極限定理 central limit theorem 統計用語集 統計WEB 2023/5/5閲覧
Mann-Whitney U 検定と並べ替え検定:小標本の正確検定 生物科学研究所 井口研究室 2023/5/5閲覧
Permutation test 統計ソフトRの備忘録 2023/5/5閲覧
Permutation test 株式会社ダイナコム 2023/5/5閲覧