今回はProphetという時系列データをモデル化するPythonのライブラリを使って時系列予測を行います。
データとしては、1949-60年の米国の旅客機の月次搭乗旅客数を記録した AirPassangers というデータセットを使用しました。
はじめに今回使用するProphetとデータセットについてそれぞれ確認してから、実際にProphetで予測を行い、結果の可視化まで行いました。
目次
Prophetとは
ProphetはFaceBook(Meta)によって開発されたライブラリで、時系列予測モデル作成に使われます。
ARIMAやSARIMAといった従来の自己回帰型の時系列予測モデルではトレンドや季節性(周期性)に関するパラメータを手動で設定する必要があるのに対し、Prophetでは自動的にトレンドや季節性を検出できます。
Prophetで使われているのは、一般化加法モデル(GAM, Generalized Additive Models)というモデルです。
GAMは変数ごとに予測値に対する寄与分を項として足していき、和を取ることで予測値を算出します。
このように項を足していくため「加法」モデルといいます。
Prophetでは4つの項を足した和から予測値を算出しています。
①トレンドの項と②周期性(季節性)の項、③イベントなどの突発的な例外事象に関する項、④誤差項です。
数式は以下に記載しています。
メモ
Prophetの予測モデル
y=g(t)+s(t)+h(t)+ϵ
y(t):予測する変数
g(t) :トレンドの項
s(t) :周期性の項(季節性、週や年ごとのサイクルなど)
h(t) :イベント効果の項(年末年始やクリスマスなど)
ϵ_t :正規分布に従う誤差項(ランダムなノイズ)
今回は公式のドキュメントのチュートリアルを参考に、必要な箇所をかいつまみながら予測を行いました。
データセット(AirPassangers)
今回はKaggleのAirPassangersという有名なデータセットを使用しました。
1949-1960年の米国の旅客機の月間搭乗者数のデータ(Air Passangers)です。
年月と人数のテーブル1つだけの単純で非常に小さなデータセットなので、動作確認用にはちょうどよいデータです。
1960年1月の乗客数が417となっており、単位(千人など)の記載がありません。
データの取得元ページにはデータに関する説明がほとんどありませんので、次の文献の年間乗客数と比較しました。
参考文献:AIRLINES GEAR FOR NEW TRANSPORTATION SYSTEM
その結果、どうやらAir Passangersのデータの単位は「万人」のようです。
1960年1年間の旅客機搭乗者数は参考文献では579万人、Air Passangersデータセットでは571万人となりました。
年によっては数値にそこそこ乖離が見られますが、そこは集計対象・方法の差かと思われます。
1950年代の航空

前段が長くなっていますが、予測を行う前に(多少なりとも)背景知識を仕入れておきます。
ドメイン知識があることは、処理の選択や結果の考察に役立つ可能性があります。
そこで、データセットの期間である1950年代の旅客機について簡単に確認します。
第二次世界大戦下の米国では、軍用機のみならず民間用の輸送機としても航空機が大量に生産・運行され、その安全性が確立されました。
このことがきっかけで、戦前までの飛行艇(水面で離発着する旅客機)による航空輸送から陸上で発着するプロペラ機による輸送に置き換わりました。
1950年当時の航空機は一般庶民には高嶺の花で、一部の富裕層や企業の重役など一部の人々の利用に限られ、一般市民が利用する機会はそうありませんでした。
まだまだ利用者層は限られるとはいえ、着実に旅客機が社会へ浸透していった時代でした。
技術革新も続き、航空機への与圧室の採用が進み、酸素濃度が低いが気流が安定する高高度を飛行するようにったり、1952年にはジェット機(デ・ハビランド コメット)の商用運行が開始されました。
しかし、現在と比べると安全性は十分に確立されておらず、1950年代前半には就航したばかりのジェット機が相次いで事故を起こして忌避されていました。
ジェット機はプロペラ機よりも定員を増やすことができるなどのメリットも有りましたが、事故をおこして危険というイメージが残り、1950年代はまだまだプロペラ機が主流の時代でした。
しかし、1957年以降は航空機メーカー各社の定員100名を超える大型ジェット機の初飛行が相次いで次第にその経済的な優位性が鮮明になるなど、新しい時代の芽が垣間見える時代でした。
Prophetによる時系列予測
ここからは、Prophetを使って時系列予測を行います。
Prophetのインストール
Minicondaで仮想環境を構築し、condaでインストールしました。
古い情報だと "conda install fbprophet" とコマンドが書かれていることがありますが、PythonのVersion 3.9.1以降では以下のコマンドでインストールする必要があります。
conda install prophetデータの可視化
モデルを作成する前にデータを可視化してみます。
import pandas as pd
import matplotlib.pyplot as plt
# 各月のデータはその月の1日目のデータとみなす
df['Month'] = pd.DatetimeIndex(df['Month'])
# Prophetの入力に合わせる
df.rename(columns={'Month':'ds', '#Passengers':'y'}, inplace=True)
# 可視化
fig, ax = plt.subplots(figsize=(12, 8))
ax.plot(df['ds'], df['y'])
ax.set_ylabel('Monthly Number of Airline Passengers')
ax.set_xlabel('Date')
# 日本語でも文字化けしないフォントを指定
ax.set_title('米国の月間航空機搭乗者数推移(1949-1960年)', fontname = 'MS Gothic')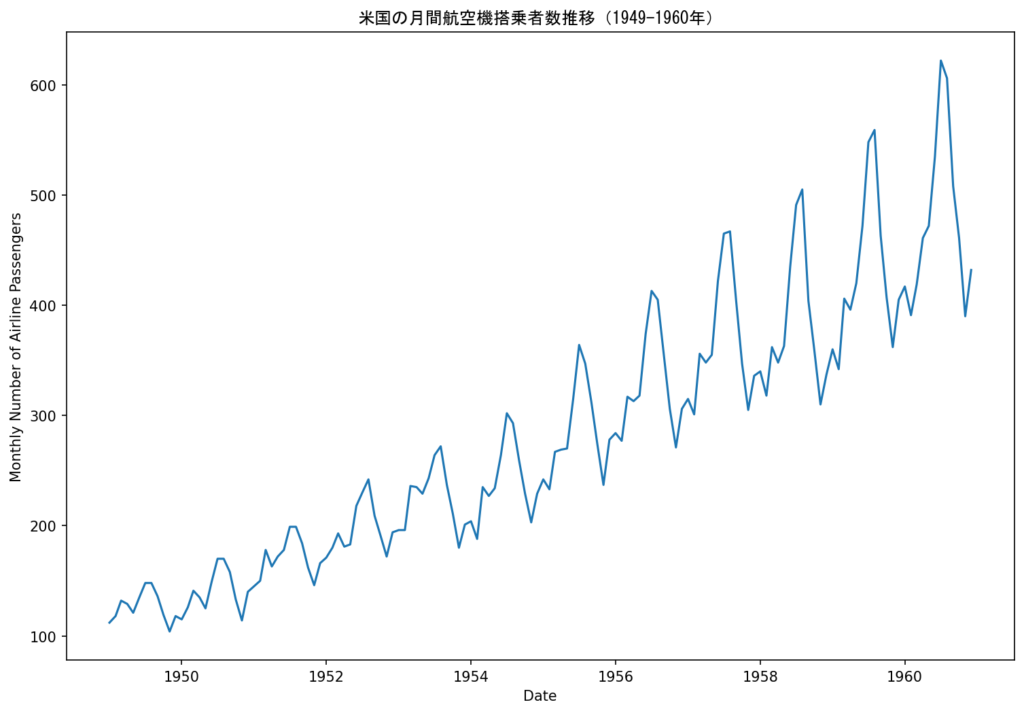
期間の最初から最後まで、1年ごとの周期性(季節性)をもちながら、きれいな右肩上がりの推移になっています。
季節性は毎年11月頃に少なく、7-8月頃に多くなるサイクルになっています。
季節による上下動は、期間の最初よりも最後の方が大きいように見えます。
モデルの作成
Prophetを使って実際にモデルを作って予測を行います。
今回は、データ数も少ないので精度検証は一旦無視して、全期間のデータを使って60ヶ月先まで(1961年1月~1965年12月)予測を行います。
from prophet import Prophet
# model fitting
m = Prophet()
m.fit(df)
# 60ヶ月先まで予測
future = m.make_future_dataframe(periods=60, freq='MS')
forecast = m.predict(future)
# 予測結果を可視化
fig = m.plot(forecast)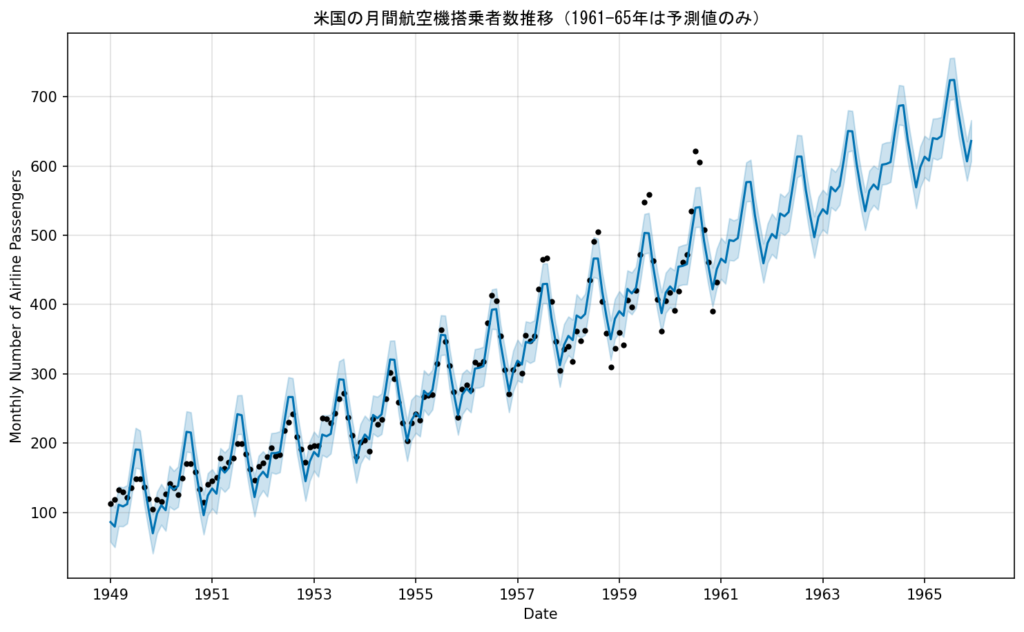
簡単なコードで予測・可視化まで行うことができました。
上昇トレンドや季節変動も反映できています。
しかし、よく見ると季節変動に誤差が発生しており、期間の前半は季節変動が実際よりも大きく予測し、期間の後半では実際よりも小さく予測してしまっています。
これは、季節変動を表す周期性の項に上昇トレンドが反映されていないことが原因です。
そこで、Prophetのインスタンス作成時に引数 seasonality_mode='multiplicative' と指定して周期性の項にもトレンドを反映させます。
次の項目で再予測を行います。
パラメータ修正
周期性の項にもトレンドが反映されるように修正して再予測を行います。
# seasonality_modeを設定
m2 = Prophet(seasonality_mode = 'multiplicative')
m2.fit(df)
# 予測
future2 = m2.make_future_dataframe(periods=60, freq='MS')
forecast2 = m2.predict(future2)
# 予測結果を可視化
fig = m2.plot(forecast2)
plt.ylabel('Monthly Number of Airline Passengers')
plt.xlabel('Date')
plt.title('米国の月間航空機搭乗者数推移(1961-65年は予測値のみ)', fontname = 'MS Gothic')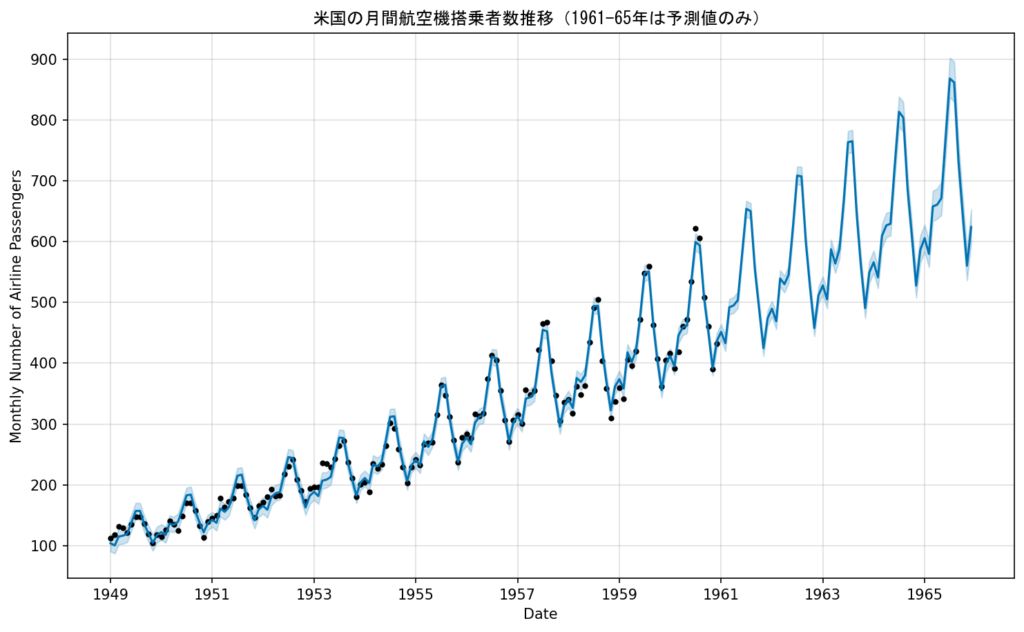
周期性の項にもトレンドが反映するようにインスタンスの書き方を変えて再予測行いました。
その結果、上の図を見てわかるように、実際の変動に対するモデルの当てはまりが目に見えて改善しています。
トレンドの項と周期性の項を出力することもできます。
# トレンド項と年周期可視化
from prophet.plot import plot_components_plotly
fig = m2.plot_components(forecast2)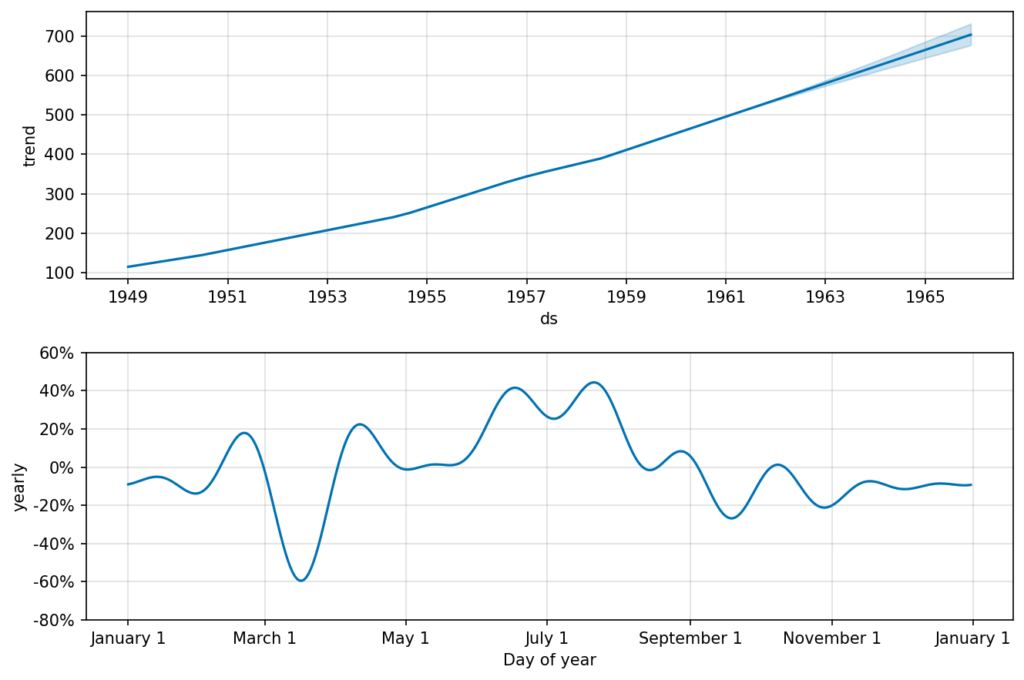
トレンドの項は期間を通して増加傾向を維持し、実際のデータと同じ傾向です。
期間の前半(54年頃まで)と後半(55年以降)では、後半のほうが増加の傾きが大きくなっているように見えます。
一方、周期性は毎年秋から冬頃に少なく、7月頃に多い傾向になっています。
実際のデータは11月頃に極小、7-8月頃に極大になるサイクルなので、若干異なりますが大きな季節変動は捉えられています。
細かい変動については実際の挙動に合わない箇所も見られます。
これは、月間データを毎月1日のデータと見なしているため少ないデータで毎日の変動をモデル化しているためです。
トレンドと変化点を追加
時系列推移にトレンドの項と変化点を追加しました。
# トレンドと変化点を追加
from prophet.plot import add_changepoints_to_plot
fig = m2.plot(forecast2)
a = add_changepoints_to_plot(fig.gca(), m2, forecast2)
plt.ylabel('Monthly Number of Airline Passengers')
plt.xlabel('Date')
plt.title('米国の月間航空機搭乗者数推移(1961-65年は予測値のみ)', fontname = 'MS Gothic')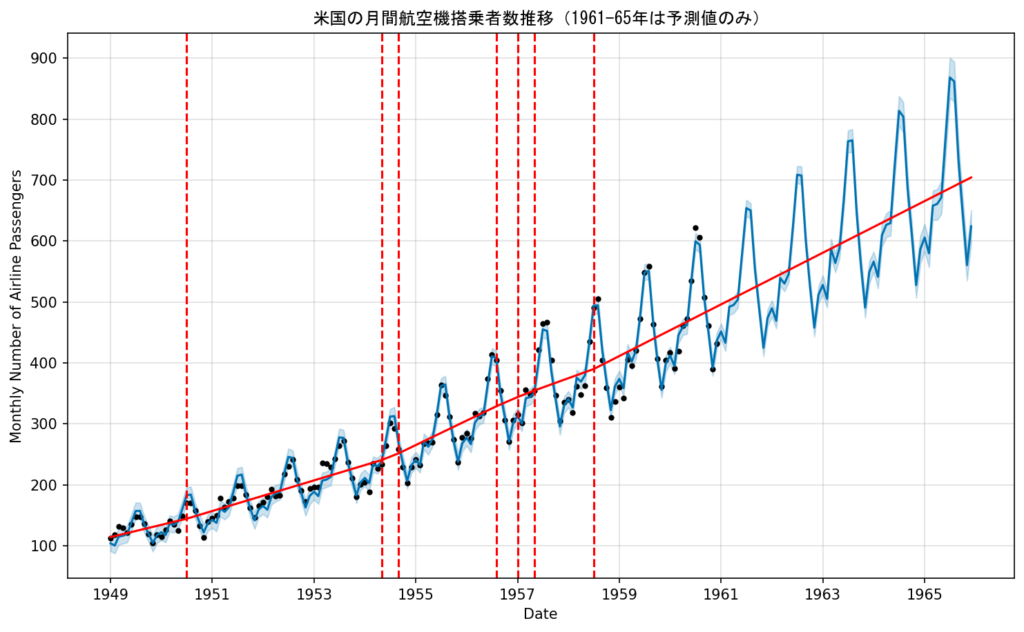
期間中いくつかの変化点があり、その前後では傾きが変わっています。
1954年の変化点以前は増加傾向であっても傾きが小さいのに対し、1954年の変化点以降、特に1958年以降は傾きが大きくなっています。
1958年は航空機メーカー各社のジェット機の初飛行が相次いだ頃であり、従来のプロペラ機よりも定員が多いジェット機の導入に伴って、搭乗者数の増加トレンドが加速したと考えられます。
参考文献
Quick Start, Prophet 2023/1/28閲覧
Sean J. Taylor and Benjamin Letham "Forecasting at Scale" PeerJ Preprints (2017)
将来予測で用いられるライブラリ「Prophet」 スキルアップAI株式会社 2023/1/28閲覧
一般化加法モデルとは? [Day19] トタデータブログ 2023/1/28閲覧
Air Passengers, Kaggle 2023/1/28閲覧
AIRLINES GEAR FOR NEW TRANSPORTATION SYSTEM, Air Transport Facts and Figures, THE AIR TRANSPORT ASSOCIATION OF AMERICA, 5-7 (1965)
ダグラス DC-6 ウィキペディア 2023/1/29閲覧
旅客機 ウィキペディア 2023/1/28閲覧
デ・ハビランド DH.106 コメット ウィキペディア 2023/1/28閲覧
ボーイング707 ウィキペディア 2023/1/28閲覧