時系列分析にて予測を行う際には、時系列データを複数の成分に分解します(時系列分解)。
このページでは、時系列分解の各成分(季節成分・トレンド成分・残余成分)と加法分解・乗法分解について解説します。
時系分解
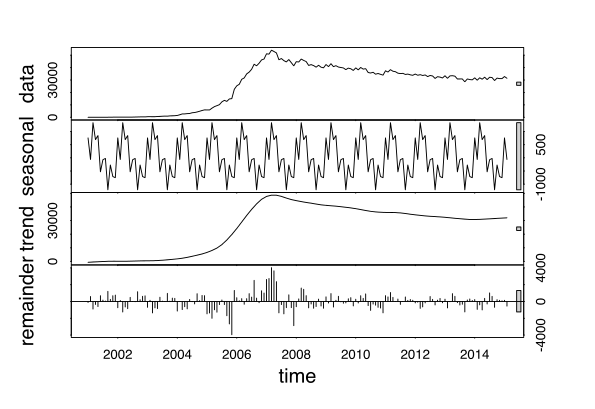
英語版Wikipediaのアクティブユーザー数の時系列分解。上から順に元データ、季節成分、トレンド成分、残差成分である。季節成分では周期的な変動が見られ、トレンド成分では2005-2007年にかけての急上昇が見られ、残差成分を見ると2005-2007年付近はノイズが大きくなっている。出典:Wikimedia Commons, CC0, 2024/5/13閲覧
時間の経過とともに値が変化するデータを時系列データといいます。
時系列データの例として、天候データや小売店の売上高や上場企業の株価などがあります。
このような時系列データでは、過去の値の変化を分析することで未来の値を確率的に予測することができます(時系列分析)。
そこで、データの時間変化に伴う値の変動要因を統計的な手法を使用して分解し、将来の値を予測する試みが様々な分野の研究やビジネスで行われます。
時系列成分
過去の時系列データを分析するにあたって、時系列データの値をいくつかの成分に分解して予測を行います(時系列分解)。
時系列データを構成する成分には以下のようなものがあります。
トレンド成分:値が長期的に増加/減少する性質を表した成分。
季節成分:日付や曜日などの周期的な変動(季節性)の影響を表した成分。
循環成分:値が周期的に上昇と加工を繰り返す性質(サイクル)を表した成分。周期が固定の場合は季節成分であり、周期が定まらないものを循環成分という。
残余成分:上記以外のランダムなばらつき(ノイズ)を表した成分。
上記のうち循環成分についてはトレンド成分に吸収させて、以下のように3つの成分で時系列データを表すことができます。
$$ y_t = S_t + T_t + R_t $$
ここで、$ y_t $ はデータの値、$ S_t $ は季節成分、$ T_t $ はトレンド成分(循環成分を内包)、$ R_t $ は残余成分です(いずれも時刻 $ t $ における)。
加法分解と乗法分解
先程の式では分解した3つの成分($ S_t, T_t, R_t $)を足し算でつないでいるため加法分解といいます。
加法分解は、季節成分やトレンド成分の変動幅がデータの値の大きさの影響をあまり受けない場合に適した手法です。
一方、値の大きさとと季節変動の振れ幅に相関がある場合は乗法分解が適しています。
乗法分解とは、分解した3つの成分($ S_t, T_t, R_t $)を掛け算でつないだ以下のような表現を指します。
$$ y_t = S_t × T_t × R_t $$
株価などの経済分野の時系列データは、前日(前年)比何%といった動きをするので、乗法分解が一般的です。
STL分解
時系列データを3成分($ S_t, T_t, R_t $)に分解する汎用的な手法として、STL分解があります(STLは“Seasonal and Trend decomposition using Loess”の略)。
従来型の手法(古典的分解やSEATS法、X-11法)と比較して、STL分解には以下のようなメリットがあります。
・様々な周期性(季節成分)をモデルに組み込む事ができる
・季節成分の時間推移による変化率を調整可能
・トレンド成分や循環成分の平滑さも調整できる
・外れ値に対してロバスト
一方、STL分解には以下のようなデメリットがあります。
・営業日数の変動や暦変動を自動的に扱えない
・加法分解のみ可能(乗法分解できない)
ただし、乗法分解についてはデータを最初に対数変換し、加法分解後に元のスケールに逆変換することで対応できます。
$ 0 \leq \lambda \leq 1 $ で Box-Cox変換を行うことで、加法分解と乗法分解の中間的な分解にも対応できます。
$ \lambda = 0 $ の場合は乗法分解、$ \lambda = 1 $ の場合は加法分解に対応します。
参考文献
時系列分析 | 用語解説 株式会社野村総合研究所(NRI) 2024/5/13閲覧
R. J. Hyndman and G. Athanasopoulos, 予測: 原理と実践 (第3版) 2024/5/13閲覧
時系列データの予測モデルについて解説! DeepSquare 2024/5/13閲覧