【巡回セールスマン問題】車内広告の問題を解いてみた

点在する都市をどのような順序でまわれば最も効率が良いかという問題を巡回セールスマン問題（Traveling Salesman Problem, TSP）といいます。
ここでは、車内広告で見かけた問題を例に、巡回セールスマン問題について学んでいきます。

車内広告@東急目黒線

上の写真は東急目黒線で見かけた車内広告です。
東急電鉄の持株会社である東急株式会社の「URBAN HACKS」というDXプロジェクトを担う組織の求人広告です。
エンジニア向けの募集広告らしく、組み合わせ最適化問題の一種である巡回セールスマン問題が掲載されています。

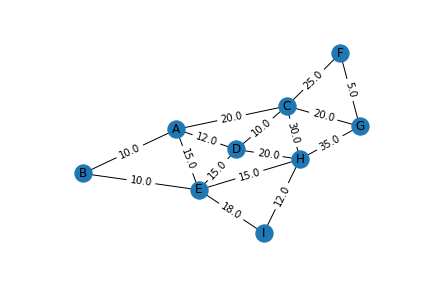
問題としては、東急の営業エリア内に点在する9つの公園すべてを訪れて出発地点に戻ってくる最短ルートを求めるというものです。
９つの公園とその間の所要時間が記載されたグラフ（ネットワーク）が与えられています。
グラフは完全グラフ（全てのノード（頂点）間にエッジ（線）が存在）にはなっていません。
そのため、あるノードから他のノードへ移動する場合はグラフ上でエッジが存在するノードにしか移動することができないという制約があります。

先に答えを書いてしまうと、
F→C→D→A→B→E→I→H→G→F
となります（どこからスタートしても同じ）。

今回は、この車内広告の問題を解きながら、巡回セールスマン問題について学んでいきます。

巡回セールスマン問題とは

巡回セールスマン問題（Traveling Salesman Problem, TSP）は、点在する都市をどのような順序で訪れれば最も距離（今回は所要時間）が短くなるかという問題です。

この問題は組み合わせ最適化問題の一種で、厳密な最適解を求めるのが難しいことで知られています。
都市の数が増えるととりうるルートの数が爆発的に増えて、スパコンでも全数探索ですべての候補を調べることが困難になるためです（NP困難）。
そのため、近似解を求める方法が知られています。

巡回セールスマン問題の近似アルゴリズム

巡回セールスマン問題の近似解を求める方法として、以下の4種類を簡単に解説します。
１．ランダムサーチ（Random Search）
２．山登り法（Hill Climbing, HC）
３．焼きなまし法（Simulated Annealing, SA ）
４．遺伝的アルゴリズム（Genetic Algorithm, GA）

今回の問題では、最後の遺伝的アルゴリズムを使って計算しています。

ランダムサーチ（Random Search）

ランダムサーチでは、ランダムに経路を作成することを繰り返し、作成した経路の中で最短の経路を近似解とみなします。
局所最適解にとらわれずに全体探索を行えるのが長所ですが、それまでの探索結果を活かすことができない非効率な手法であり、都市の数が多くなるにつれて計算時間を大きく増やさないと適切なルートを見つけることができなくなります。
理論上は、時間を無視すれば最適解にたどり着くことができますが、都市の数が多い問題では現実的ではありません。

山登り法（Hill Climbing, HC）

山登り法は、現在分かっている最短経路の一部をランダムに別ルートに置き換えてみて、より短い経路が見つかれば最短経路を更新するという手法です。
局所探索法の一種であり、局所的に最適なルートを探していきます。
そのため、最初にどのような経路から探索を始めるかに最終的な解（見つけ出した最短経路）が依存し、局所最適解に陥りやすい方法です。

焼きなまし法（Simulated Annealing, SA ）

焼きなまし法はアニーリングともよばれ、山登り法の欠点である局所最適解に陥らないような工夫がなされた手法です。
焼きなまし法では、山登り法同様に一部をランダムに別ルートに置き換えて最短経路を探していきますが、最短経路でなくても一定確率で更新します。
最初は別ルートに置き換える確率を高くしておき、回を重ねるごとに次第に確率を下げて収束させていきます。
この過程が、熱してやわらかくなった金属をゆっくり冷却することでムラがなく均一な結晶にする処理（焼きなまし、アニーリング）と似ていることから、焼きなまし法とよばれています。

焼きなまし法では、別ルートに置き換える確率を下げていくスピードが短いほど計算時間が短くなりますが、あまりに急激に下げると結果的に山登り法と同じような解に収束します。
焼きなまし法は局所最適解にとらわれずに大域的な探索を行うことができますが、一方で別ルートに置き換える確率を下げていくスピードの調整に経験的な調整が必要になります。

遺伝的アルゴリズム（Genetic Algorithm, GA）

遺伝的アルゴリズムは、生物の遺伝子の進化を模したアルゴリズムで最適解の探索を行うものです。
都市の訪問順の並びを遺伝子の配列に見立て、その配列に対して様々な遺伝子操作を行うことで最適解を探索する方法です。

遺伝的アルゴリズムは、現実の生物群集のように様々な遺伝子パターンをもつ個体群を作り出し、それに対して適合度（今回は経路の短さが尺度）の評価を行い、次の世代の個体群を作り出していくという特徴をもちます。
山登り法や焼きなまし法は現時点の最短経路１つを情報として保持しながら解を更新していきましたが、遺伝的アルゴリズムでは一世代で複数の経路を情報として保持しながら、最短経路の解に近づくように探索していきます。

遺伝的アルゴリズムにおける遺伝子操作としては、 選択（淘汰）、交叉（こうさ）、突然変異の３種類があります。
中でも交叉は生物の遺伝子の相同組換えを模した操作で、遺伝的アルゴリズムの特色が出る操作になります。

選択（淘汰）

選択（淘汰）は、今の世代の適合度（今回は各経路の所要時間の短さ）をもとに次の世代を生み出す操作です。
選択の際には、今の世代よりも次の世代の適合度が高くなるような選び方をします。
選択には次の４種類の方法があります。

１．ランキング方式：
適合度の高い（最短経路の短い）ものから順番に次世代に残す確率を高く設定し、確率的に次世代に残す個体を選択

２．トーナメント方式：
今の世代の中から一定数の個体をランダムに選択し、その中で最も適合度の高い個体を次世代に残す（必要な個体数の数だけ操作を繰り返す）

３．ルーレット方式：
各個体に適合度に正比例した点数をつけ、適合度が大きいほど面積が大きいルーレットを回して次の世代に残す個体を選択（必要な個体数の数だけ操作を繰り返す）

４．エリート方式：
今の世代で適合度上位の一定数の個体を次の世代に残す方法。適合度の高い個体が偶然失われることを防ぐ方法であり、他の方法と併用することが前提

交叉

交叉（こうさ）は、２つの個体がもつ経路を一部を組み替えることで新しい配列の個体を作り出す操作です。
生物の遺伝子の相同組換えに着想を得た遺伝的アルゴリズムの特色ともいえる操作です。

交叉のやり方の一つとして、サブツアー交換交叉があります。
サブツアー交換交叉は、２つの経路の中で経由する都市（ノード）が共通する部分だけをピックアップし、その部分だけを組換えの対象とするものです。
組換えを行っても他の部分への影響を小さくする方法ですが、交叉点が固定されて探索があまり進まないうちに収束してしまう可能性があります。

他にも部分写像交叉 (Partially Mapped Crossover, PMX)などいくつかの手法が存在します。

突然変異

突然変異は、経路の一部をランダムに別ルートに置き換える方法で、山登り法などと同様の操作になります。
あまり突然変異を増やすと、遺伝的アルゴリズムの特色である交叉の影響が失われるのでバランスを考える必要があります。

Pythonでの実装（mlroseパッケージ）

実装には巡回セールスマン問題用の関数があるPythonのmlroseパッケージを使いました。
以下、Google Colabのコードも交えて説明していきます。

バージョン情報

# バージョン情報
!python --version
# Python 3.7.14
!pip list | grep 'mlrose'
# mlrose                        1.3.0

はじめに必要なパッケージをインポートします。

# パッケージの読み込み
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np

# mlroseをimportとする際にエラーを回避するための処理
import six
import sys
sys.modules['sklearn.externals.six'] = six

import mlrose

データの作成

はじめに、入力のデータを作成します。
画像のグラフ（ネットワーク）を見ながら手作業でエッジ（線分）とその重み（ここでは所要時間）を記載したファイルを用意する必要があります。

実際に作成したファイルの中身は以下のようになります。
エッジ（枝）を構成する２つのノード（頂点）とエッジの重みをスペース区切りで表現しています。
１行で１本のエッジを表現し、グラフを構成するすべてのエッジの情報を記載しています。

# data.txt
A B 10
A C 20
A D 12
A E 15
B E 10
C D 10
C F 25
C G 20
C H 30
D E 15
D H 20
E H 15
E I 18
F G 5
G H 35
H I 12

上のファイルを読み込んで試しにグラフを描いてみます。

# グラフの作成
g = nx.DiGraph()
# エッジリストの読み込み
file_path = 'data.txt'
g = nx.read_weighted_edgelist(file_path, nodetype=str)
# ノードの座標情報取得
pos = nx.spring_layout(g)
# エッジごとの重みの辞書を作成
edge_labels = {(i, j): w['weight'] for i, j, w in g.edges(data=True)}
# 重みの表示
nx.draw_networkx_edge_labels(g, pos, edge_labels=edge_labels)

# グラフ描画
nx.draw_networkx(g, pos, with_labels=True, alpha=1)
# グラフ表示
plt.axis('off') # 枠線非表示
plt.show()

描画したグラフは次のとおりです。

冒頭の車内広告に記載のグラフと各ノードの配置が異なるのは、あくまでノード間の重みだけをもとに描画したためです。
グラフ（ネットワーク）では、画像の上下左右どこに描画されるかは意味のある情報ではありません。
グラフが表現している情報は、どのノード間にエッジがあるかとエッジの重みのみです。

最短経路の探索

ここからは、mlroseパッケージを使って、遺伝的アルゴリズムにより最短経路を探索します。

今回入力としているデータではノードの名前がアルファベット１文字で表現されています。
mlroseでは入力データのノードを0, 1, 2, 3, …というようにゼロはじまりの数値で表現する必要があります。
まず前処理として、アルファベット１文字で表記されたノード名を数値に変換し、mlroseの入力用データを作成します。

# ノード名一覧
node_list = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']


# 関数定義：アルファベットを数字に変換
# 【注意】nodeを数字に置き換える際に、0スタートの連続な整数値にしないと mlrose.TravellingSales実行時に下記エラーが出る
# Exception: All nodes must appear at least once in distances.

def alpha2num(chr_list, node_list):
  # アルファベットを数字に変換
  for i in range(len(chr_list)):
    # ノード名は数字へ
    if (chr_list[i] in node_list):
      chr_list[i] = ord(chr_list[i]) - ord('A')
    # 距離（数値）は数値型へ
    else:
      chr_list[i] = float(chr_list[i])
  
  return(chr_list)


# fitness関数用にエッジリストの読み込む
file_path = 'data.txt'
with open(file_path, 'r', encoding='cp932') as f:
    # リストとして読み込む
  lines = f.readlines()
# 改行コード削除
lines = list(map(lambda s:s.rstrip("\n"), lines))

# エッジリストをfitness関数入力用の形式に調整
edge_list = []
for i in range(len(lines)):
  edge_info = lines[i].split(' ')
  # 文字列を数値に変換
  edge_info = alpha2num(chr_list=edge_info, node_list=node_list)
  edge_info = tuple(edge_info)
  edge_list.append(edge_info)

print(edge_list)

ここで作成したedge_listは次のようにエッジを構成する２つのノードとエッジの重みからなるタプルのリストになっています。

[(0, 1, 10.0), (0, 2, 20.0), (0, 3, 12.0), (0, 4, 15.0), (1, 4, 10.0), ・・・]

いよいよ最短経路の探索に入ります。
まず、edge_listを入力としてfitness関数を作成します。

fitness関数は、巡回セールスマン問題において制約条件を満たした経路に対して、巡回したノードや経路全体の重み（今回は所要時間）を評価する関数です。

# エッジ情報からfitness関数作成
fitness_dists = mlrose.TravellingSales(distances = edge_list)

次に最適化問題オブジェクトの作成です。
fitness関数の情報に加えて、訪問都市数や最短経路と最長経路どちらを求めるのかといった情報を追加します。

# 最適化問題オブジェクト作成
problem_fit = mlrose.TSPOpt(length = len(node_list),
                            fitness_fn = fitness_dists, 
                            maximize=False
                            )

そして、遺伝的アルゴリズムにより最短経路の探索の探索を行います。
mlroseのgenetic_alg関数では、各世代からランダムに選んだ2種類の親配列から交叉により次の世代の配列を作り出します。
これを各世代のn数分だけくりかえし、次の世代の個体群を作り出します。
新しい世代の配列の中で最も距離（今回は所要時間）が短い配列を探し、前の世代よりも距離が短くなった場合は最短経路を更新します。

# 遺伝的アルゴリズムによる最短経路の探索
best_state, best_fitness = mlrose.genetic_alg(
    problem_fit, # 最適化問題オブジェクト
    pop_size = 200, # 各世代のn数 
    mutation_prob = 0.2, # 突然変異の発生確率
    max_attempts = 100, # 世代の数
    random_state = 2
    )

print(best_state)
# [5 2 3 0 1 4 8 7 6]
# [F C D A B E I H G] # 出力した頂点をアルファベット表記に戻した場合

print(best_fitness)
# 137.0

以上より、最短経路は次のように求まりました。

F→C→D→A→B→E→I→H→G→F

スタートがF（二子玉川公園）なのは偶然であり、random_stateで指定する乱数値によって変わります。
周回ルートなので、どのノードからスタートしてもルートは同じです。

今回は遺伝的アルゴリズムによって解きましたが、同じmlroseパッケージには、山登り法（hill_clim関数）や焼きなまし法（simulated_annealing関数）が存在し、遺伝的アルゴリズム（genetic_alg関数）以外のアルゴリズムで解くこともできます。

最短経路を地図にマッピング

最後に作成した最短経路をGoogle Map上にマッピングしてみました。
西側の（Ｊ）二子玉川公園がスタート/ゴール地点で、青線はGoogle Mapによる推奨経路（徒歩）です。
なお、地図上のアルファベットは公園の訪問順で、元のノードとはアルファベットが対応していません。

地図上で見ても、無駄が少ないルートで巡回していることがわかります。
今回はノード（公園）の数が少ないため、地図があれば人間が目で見ても直感的に訪問順を決めることができそうですが、ノードの数が増えて直感的に最適解がわかりづらい配置になっても今回のアプローチで最短経路を探すことができます。

参考文献

mlrose: Machine Learning, Randomized Optimization and SEarch (GitHub) 2022/10/12閲覧
簡単そうで難しい組合せ最適化　京都大学 情報学研究科 数理工学専攻 離散数理分野 永持研究室　2022/10/09閲覧
鳥居鉱太郎「お遍路における巡回セールスマン問題」(download) 松山大学論集 23(3), 89-101 (2011)
巡回セールスマン問題と遺伝的アルゴリズム(GA)　株式会社スタジオ・ケイ　2022/10/09閲覧
焼入れ・焼もどし・焼なまし・焼ならし　株式会社キーエンス　2022/10/09閲覧
遺伝的アルゴリズム　東京大学 情報理工学系研究科 電子情報学専攻 伊庭研究室　2022/10/09閲覧
遺伝的アルゴリズムに関する基礎知識を解説　FEnetインフラ　2022/10/09閲覧
前川景示他「遺伝アルゴリズムによる巡回セールスマン問題の一解法」計測自動制御学会論文集 31(5), 598-605 (1995)
片山謙吾、成久洋之「遺伝的アルゴリズムの効率的交叉法について」(download) 岡山理科大学紀要. A, 自然科学 33, 233-245 (1997)