線形回帰における２つのアプローチ（最急降下法と正規方程式）

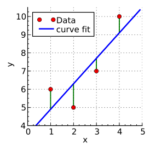
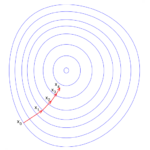
データの変動をモデル化して説明する手法の１つとして線形回帰があります。
線形回帰は比較的シンプルな回帰モデルであり、解釈性の高いモデルです。
このページでは、実測値（データ）と予測値（回帰直線）の誤差を最小化する２つのアプローチについてまとめます。

線形回帰

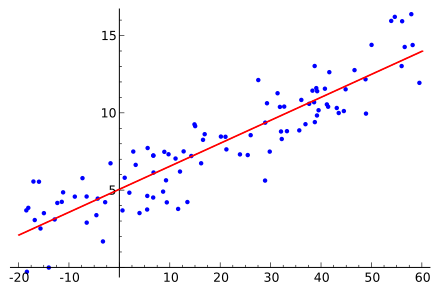
線形回帰（linear regression）とは、データの変動をいくつかの変数の和によって説明する手法です。
線形回帰を使うことで、既存のデータから未知のデータの値を予測することができます。
予測値は直線上に分布するため回帰直線として表せます。

変数の数が１つの場合（線形単回帰）、線形回帰による推定値（予測値）は以下の式で表されます。

$$ f(x) = θ_0 + θ_1 x $$

ここで、$ θ_0, θ_1 $ は定数です。

この手法で求められる推定値の関数 $ f(x) $ は直線であるため、回帰直線とよびます。
そのため、$ θ_0 $ は切片、$ θ_1 $ は傾きに相当します。

上の式は変数が１つ（ $ x $ ）のみの場合でしたが、一般化のために変数が複数ある場合（線形重回帰）を考えます。
変数の数を $ n $ とすると、線形回帰によって求められる推定値は $ f(x_n) $ は $ n $ 個の変数 $ x_1, x_2, \cdots, x_n $ を使って以下のように表現されます。

$$ f(x_{ n }) = θ_0 + θ_1 x_1 + θ_2 x_2  + \cdots +  + θ_n x_n $$

各変数は重み $ θ_0, θ_1, θ_2, \cdots, θ_n $ をかけた加重和として表現されます。

線形回帰の２つのアプローチ

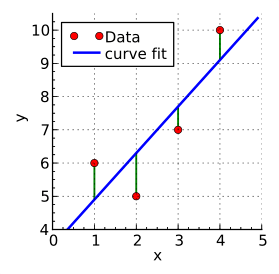
$ f(x) = θ_0 + θ_1 x $ はパラメータ $ θ_0, θ_1 $ の値次第でどのような直線でも描くことができます。
そこで、２つのパラメータの値を最適化して実測値の誤差を最小にする直線を求める必要があります。
パラメータの値は方程式を解くことで求められ、線形回帰では方程式を解析的に解く方法が用いられます。
scikit learn の sklearn.linear_model.LinearRegression でも正規方程式を用いて解析的に解いて回帰直線を求めています。

しかし、変数や次元が多い複雑な方程式になると解析的に解いて回帰直線を求めることが困難になります。
そこで、方程式を解いて回帰直線を求めるのではなく、数値計算を繰り返して探索的に誤差が最小となる回帰直線を求める方法もあみだされています。
この方法は解析的に解を求めることができない複雑な場合でも探索的に最小値を求めることができます。
その代わりに学習率というハイパーパラメータをチューニングする必要があります。

以下では、前者のような方程式を解析的に解くアプローチと後者のような数値計算による単作を繰り返して数値的に解く方法を順にまとめます。

解析的に解く方法（正規方程式）

はじめに、方程式を解くことで回帰直線を求める方法についてふれます。
このアプローチでは、実測値と回帰直線の誤差をMSE（平均二乗誤差、Mean Squared Error）によって評価します。
MSEが最小値になるときに成り立つ関係式を正規方程式をいい、正規方程式を解くことで回帰直線を求めることができます。

正規方程式による線形回帰については、以下のページで解説しています。

数値的に解く方法（最急降下法）

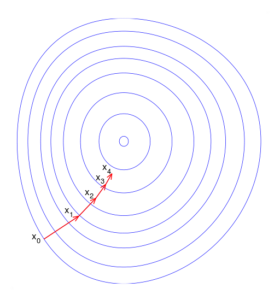
線形回帰の２つ目の方法として、初期値を決めて数値計算を繰り返して探索的に誤差が最小となるパラメータの組み合わせを求めるアプローチがあります。
このような数値的に解くことで回帰直線を求める方法として、最急降下法があります。
最急降下法では、関数上のある地点における傾きの情報を元により値が小さくなる方向へ移動し、再度傾きを計算することで最小値を探索します。
最急降下法を用いて実測値と回帰直線の誤差が最小になる回帰直線を求めます。

最急降下法を用いた線形回帰については、以下のページで解説しています。

実装

最後にscikit-learnによる線形回帰の実装例を紹介します。

はじめに、必要な関数を読み込み、線形回帰に使うデータを乱数を使って擬似的に生成します。

import numpy as np # 乱数取得用
from sklearn.linear_model import LinearRegression # 線形回帰
import matplotlib.pyplot as plt # 可視化用

# 乱数を使って擬似的に実測値データを作成
n = 100 # プロット数
seed = 1234 # 乱数のシード値
np.random.seed(seed=seed) # 乱数のシード値指定
# 説明変数
X = np.random.rand(n)
# 目的変数
y = [0.5 * xdata + 2 + np.random.randn()*0.01 for xdata in X]

sklearn.linear_model.LinearRegressionを使用して線形回帰を行います。
この関数では正規方程式を用いて解析的に解いて回帰直線を求めています。

# インスタンス生成
model = LinearRegression()
# データ整形
X = X.reshape(-1, 1)
# 学習（回帰直線生成）
model.fit(X, y)

# 回帰直線の傾きと切片の確認
# 傾き
coef = model.coef_[0]
print(coef)
# 0.49882647618900566
# 切片
intercept = model.intercept_
print(intercept)
# 2.000763063232016

# モデルによる予測(入力は学習時と同様に二次元Array)
print(model.predict([[30]]))
# [16.96555735]

回帰直線の傾きは0.499、切片は2.00となりました。
最後にデータと回帰直線を可視化して視覚的に確認します。

# グラフ描画領域を作成
fig, ax = plt.subplots()
# 乱数値をプロット
ax.plot(X, y, linestyle='', marker='o', markersize=4)
# 軸ラベル追加
ax.set_xlabel('X')
ax.set_ylabel('y')
# 回帰直線を追加
ax.axline((0, intercept), slope=coef, color='red')
# 回帰直線の式を追加
s = 'y = ' + str(round(coef, 3)) + ' x + ' + str(round(intercept, 3))
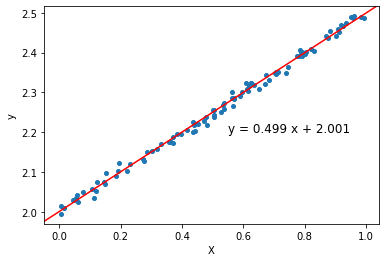
ax.text(x=0.55, y=2.2, s=s, fontsize='large')

上記コードを実行することで、次のようなグラフを得られました。

青い点は $ y = 0.5 x + 2 $ に従うように与えた乱数値なので、回帰直線は本来の分布をよく表しているといえます。

参考文献

線形回帰モデルの説明　Amazon Web Services　2024/1/15閲覧
渡邊直樹「線形回帰」慶應義塾大学 大学院経営管理研究科（2021 年 9 月 22 日 ）
1.1. Linear Models, scikit-learn　2024/1/14閲覧
sklearn.linear_model.LinearRegression, scikit-learn　2024/1/14閲覧
最急降下法と正規方程式のメリットどデメリット　蒼の王座・裏口　2024/1/14閲覧
正規方程式を完全解説(導出あり)【機械学習入門4】　米国データサイエンティストのブログ　2024/1/14閲覧
確率的勾配降下法・最急降下法・最小二乗法 - AI研究所　株式会社VOST　2024/1/14閲覧
最急降下法を図と数式で理解する(超重要)【機械学習入門3】　 米国データサイエンティストのブログ　2024/1/14閲覧