線形回帰を行う手法の1つとして最急降下法があります。
最急降下法では探索的に最も当てはまりのよい回帰直線を求めることができるため、正規方程式を用いる場合よりも少ない計算量で解くことができます。
このページでは、最急降下法について解説します。
最急降下法とは
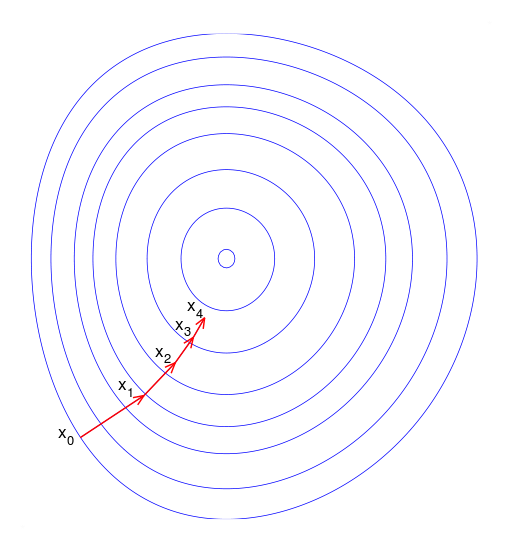
最急降下法(gradient descent, steepest descent)は関数の傾きのみから最小値(極小値)を探索するためのアルゴリズムです。
関数上のある地点における傾きの情報を元により値が小さくなる方向へ移動し、再度傾きを計算して関数上の最小値を探索します。
線形回帰においては、回帰直線とデータの誤差項(損失関数(Loss function))を最小化するために使われます。
傾きのみで最小値を探索するため簡便で計算時間が短いという特徴があります。
一方、探索地点の傾きのみの情報から探索するため、局所的な最適解(極小値)に収束してしまい、大域的な最小値にたどりつけない場合があります。
以下では、最急降下法を使って線形回帰を行う場合を考えます。
線形モデル
1変数の直線は次のように表せます。
$$ f(x) = θ_0 + θ_1 x $$
ここで、$ θ_0 $ は切片、$ θ_1 $ は傾きです。
簡略化のために1変数( $ x $ )のみを扱います。
なお、多変数を扱う場合は一般化した下記の式のようになります。
$$ f(x_{ n }) = θ_0 + θ_1 x_1 + θ_2 x_2 + \cdots + + θ_n x_n $$
損失関数(MSEを使用)
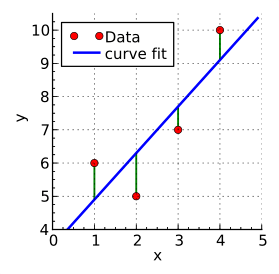
線形モデルの当てはまりを評価するためには、損失関数を定義して最小値を探索します。
線形モデル(上図青線)と実際のデータのプロット(上図赤丸)の差分(上図緑線)がモデルとデータの誤差になります。
この誤差が最小になるような直線が最も当てはまりの良い回帰直線になります。
まず、誤差を評価するために誤差項を損失関数を定義します。
誤差を評価する方法として平均二乗誤差(MSE, Mean Squared Error)を使用します。
MSEはその名前の通り、各点の誤差(推定値(回帰直線)と実測値(実データ)の差分)の二乗の平均をとったものです。
二乗することで上方向と下方向の誤差が互いに打ち消し合うのを防いでいます。
実測値(実データ)は $ y_i $ 、線形回帰による推定値 $ \widehat{ y_i } = θ_0 + θ_1 x_i $ なので、MSEは以下のように表されます。
$$ MSE = \frac{ 1 } { n } \displaystyle \sum_{ i=1 }^n \{ y_i - \widehat{ y_i } \}^2 = \frac{ 1 } { n } \displaystyle \sum_{ i=1 }^n \{ y_i - (θ_0 + θ_1 x_i) \}^2 $$
ここで、$ y_i $ は $ i $ 番目の実測値(上図赤丸)、$ x_i $ は対応する推定値(上図青線と緑線の交点)です。
全データ(1番目から $ n $ 番目まで)の全データについて誤差の二乗を求め、平均をとっています。
今回は、MSEを損失関数 $ L (θ_0, θ_1) $ として利用し、回帰直線を求めます。
$$ L (θ_0, θ_1) = MSE $$
$ L $ のパラメータが $ θ_0 $ と $ θ_1 $ なのは、これらが求めたい回帰直線の切片と傾きであるからです。
最急降下法

最急降下法では、現在の座標における損失関数の傾きを計算し、その傾きの情報から最小値を探索します。
今回は1変数の線形回帰なので、損失関数(今回はMSE)に対して2変数 $ θ_0 $ と $ θ_1 $ それぞれで偏微分を行い傾きを求めます。
$$ \frac{ \partial }{ \partial θ_0 } L (θ_0, θ_1) = \frac{ 2 }{ n } \displaystyle \sum_{ i=1 }^n \ ( θ_0 + θ_1 x_i - y_i ) $$
$$ \frac{ \partial }{ \partial θ_1 } L (θ_0, θ_1) = \frac{ 2 }{ n } \displaystyle \sum_{ i=1 }^n \ ( θ_0 + θ_1 x_i - y_i ) x_i $$
上の式より、現在の座標における傾きがわかったので、最小値を探索するために2変数 $ θ_0 $ と $ θ_1 $ の値を更新します。
たとえば、上のグラフにおいて青の接線は傾きは正なので、座標を更新する際にはマイナス方向に移動すれば最小値に近づけます。
更新後の新しい座標は、元の座標から $ L $ の偏微分をマイナスした以下のような式で表されます。
$$ θ_0 := θ_0 - η \frac{ \partial }{ \partial θ_0 } L (θ_0, θ_1) $$
$$ θ_1 := θ_1 - η \frac{ \partial }{ \partial θ_1 } L (θ_0, θ_1) $$
ここで $ := $ は左辺を右辺で定義することを表します。
新しい $ θ_0 $ と $ θ_1 $ は、更新前の値から少しだけ値をずらしています。
更新前の値からどれだけずらすかは、ハイパーパラメータである学習率 ($ η $, Learning rate )によって決まります。($ η $ は 0 から 1 の間の数値)
学習率が小さいと前回計算した座標から少ししか離れていない場所を計算するため、最小値にたどり着くまでに多くのステップを要して時間がかかります。
一方、学習率が大きすぎると前回座標から離れ過ぎた場所を計算しようとするため、最小値がある地点を飛び越えてしまう可能性が高くなり、最小値に収束しないリスクがあります。
適切な学習率を設定した上で学習( $ θ_0 $ と $ θ_1 $ の値の更新)を一定回数繰り返して収束した値を最小値とみなします。
注意点と手法の改良
最急降下法を使用する際の手法の注意点としては、損失関数が複数の極小値をもつ場合には、最小値ではない極小値(局所最適解)に収束してしまい、最小値にたどりつけない場合があることです。
これは、探索地点の傾きのみの情報から探索するためです。
このような欠点を解消するために、確率的勾配降下法(Stochastic gradient descent, SGD)といった手法も存在します。
確率的勾配降下法では、最急降下法のように損失関数の計算に全てのデータ(実測値)を用いるのではなく、ランダムに選んだ1個のデータのみで傾きを計算して更新していく方法もあります。
ただし、最急降下法と確率的勾配降下法はいずれもデータ数が多くなると計算量が増えるため、計算量を減らしたミニバッチ勾配降下法(Minibatch Stochastic Gradient Descent)という手法もあります。
ミニバッチ勾配降下法では、数~数百個程度に区切ったデータを1グループとして分割し、ランダムに選んだグループに対して傾き計算とパラメータ更新を行います。
参考文献
最急降下法 ウィキペディア 2024/1/14閲覧
Gradient descent, Wikipedia 2024/1/14閲覧
確率的勾配降下法・最急降下法・最小二乗法 - AI研究所 株式会社VOST 2024/1/14閲覧
最急降下法を図と数式で理解する(超重要)【機械学習入門3】 米国データサイエンティストのブログ 2024/1/14閲覧
Learning rate, Wikipedia 2024/1/21閲覧
How to Configure the Learning Rate When Training Deep Learning Neural Networks, Machine Learning Mastery 2024/1/21閲覧