河川の水位の予測は防災の観点から重要ですが、大小様々な河川の予測はその複雑性や観測地点の不足から難しいタスクです。
ここでは、降水量から河川水位を予測するアプローチについて概観し、手法の選択肢をまとめます。
目次
降水量と河川水位

降水と河川の形成(英国・スコットランド西部の丘陵地帯Luss Hills)。流域一帯に降った雨が低い方向へ流れながら川筋を形成しながら下流へ流れていく。出典:Wikimedia Commons, ©Michal Klajban, CC BY-SA 4.0, 2022/12/24閲覧
雨が降ると川の水位が上がるのは当たり前の話ですが、その場所の降水量だけから河川水位を予測することは簡単ではありません。
地表に降った雨は低いところに集まりながら次第に川を形成し、いくつもの川筋が合流して大きくなりながら海に流れます。
この過程で、一部の水は地下へ浸透して地下水となり、また植物に吸収されたり蒸発により失われます。
その一方で、雪解け期には冬の間に地表に降り積もった雪が少しずつ溶けていき、河川流量を増やす要因となります。
このように、単純に降水量と河川を流れる水の流量はイコールにはなりません。
加えて、上流で降った大雨と観測地点で降った大雨では、増水するタイミングも異なります。
遠く離れた上流で降った雨ほど河川を流れるのに時間がかかるため、観測地点の水位に反映されるのも遅くなります。
そのため、ある時刻の水位は、その場所のその瞬間の降水量に加えて、上流の時間差の降水量が影響してきます。
以上の特性は、河川や観測地点ごとに表れ方が変わります。
このため、降水量から河川水位を予測するためには、その河川の上流域の降水量や水位の経時変化の情報に加え、河川ごとの特性を学習する必要があります。
ハイドログラフ
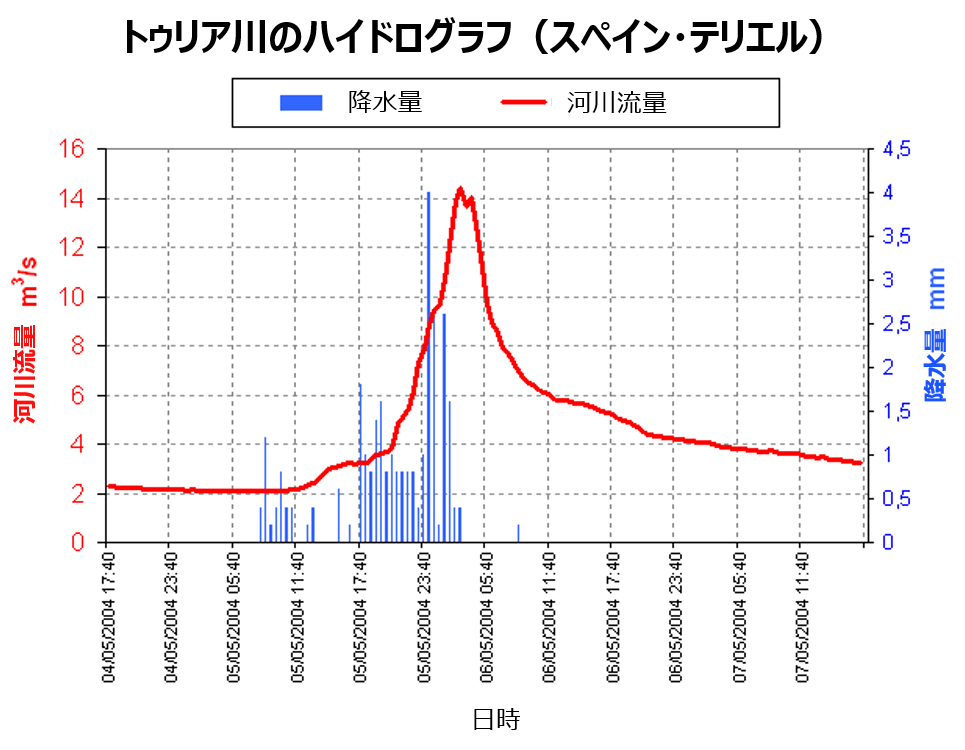
ハイドログラフの例(スペイン・テルエル・トゥリア川)。横軸は時間であり、青字と棒グラフは降水量(mm)、赤字と折れ線グラフは河川流量(mm/s)を表している。降水量からやや遅れて河川流量のピークが到来する。出典を加工して作成。出典:Wikimedia Commons, ©FerranTatachan, CC BY-SA 4.0, 2022/12/17閲覧
ハイドログラフは、横軸に時間をとり、河川の流量や水位などの時系列推移を可視化したグラフです。
上図では、降水量と河川流量の時系列推移を表しています。
雨が降りはじめるとやや遅れて河川流量が上昇しはじめますが、降水のピークに遅れて河川流量のピークがやってきます。
これは、観測地点より上流で降った雨が時間差で流れてきたからです。
上流の影響がどのように表れるかは河川によって変わってきます。
降水量から河川水位を予測するためには、河川や観測地点ごとに降水量と河川流量や水位の関係性を見出す必要があります。
河川水位の予測方法
流域の降水量からある地点の河川水位を予測する方法は、流出解析モデルと過去データを用いた統計モデルの2つに大別できます。
流出解析モデルは水の動きをモデル化した解釈性の高い水文学的な手法であるのに対し、統計モデルは関係性はブラックボックスながら限られた情報から予測できる方法です。
流出モデルを使用する方法
1つ目の流出解析モデルを使用する方法は、河川の水の動きをモデル化しているため解釈性の高い方法です。
水の流れをモデル化するために必要となるデータの種類は増え、必要なパラメータも多くなります。
この方法では、はじめに降水量などから河川流量を算出し、次いで河川流量から地点ごとに水位を求めます。
地表への降水量と元々からある貯水量から河川流量を算出する際に流出モデルを使用します。
流出モデルは、ある地点に元からある貯水量に対して、降水や蒸発による増減を考慮した上でその地点からの流出量=河川流量を推定するための数理モデルです。
流出モデルを扱うためには、流域の多くの地点の時間ごとの降水量や流出量などのデータが必要になります。
代表的な流出モデルとして、貯留関数法やタンクモデルがあります。
次にある地点の河川流量から河川水位を求めます。
流量と水位の関係は地点ごとに変わるため、堰などを設置して測定する必要があります。
流量と水位の関係は水位上昇期と下降期で異なり、上昇期の方が同じ水位でも河川流量が多くなります。
流量と水位の関係をグラフにプロットしたものをH-Q曲線といいます。
縦軸に水位(Height)と横軸に流量(Quantity)をとり、平常時から降雨により増水し、やがて減水して平常に戻るまでの一連の水位と流量の変化を線でつないでプロットします。
以上のアプローチは複雑で必要なデータが増える代わりに、地点ごとの貯水量や蒸発量など様々な関連事象を説明することができます。
加えて、過去データに依存せずに河川水位を予測できるという利点もあります。
過去データを用いた予測
2つ目の方法は、Nearest-Neighbor法(k近傍法)やニューラルネットワークにより過去データを学習させて河川水位を予測する方法です。
このアプローチでは、流域における複雑な水の動きの把握は一旦おいておき、過去データのパターンを学習することで水位を予測します。
誤差評価には、通常RMSE(Root Mean Squared Error, 二乗平均平方根誤差)が使用されます。
一例としてNearest-Neighbor法では、流域全体の流量が正確にわからなくても、少数の観測地点の降水と河川水位のパターンのデータが集まれば、ある程度の精度で水位を予測できます。
そのため、観測地点の少ない中小河川にも適用でき、解釈性よりも実用性を優先した方法と言えます。
ただし、このアプローチで予測精度を高めるには十分な期間の観測データが必要です。
Nearest-Neighbor法を用いて淀川流域(近畿)の流量予測を行った研究(藤原ら 2003)では、1-3日後の流量の予測精度はデータが1年分しかない場合に際立って悪いため、データは最低でも2年分以上は必要であると考えられます。
雨量から水位を予測する他のアプローチとして、ニューラルネットワークを使用して雨量から河川流量を介さずに直接河川水位を予測する試みも行われています。
Nearest-Neighbor法を用いた予測手法に関する日本語の論文は2000年代初頭までが中心ですが、ニューラルネットワークを用いた手法は2010年代も盛んに投稿されています。
以下では、河川水位予測に使われているニューラルネットワークの手法についてかんたんに紹介します。
順伝播型ニューラルネットワーク
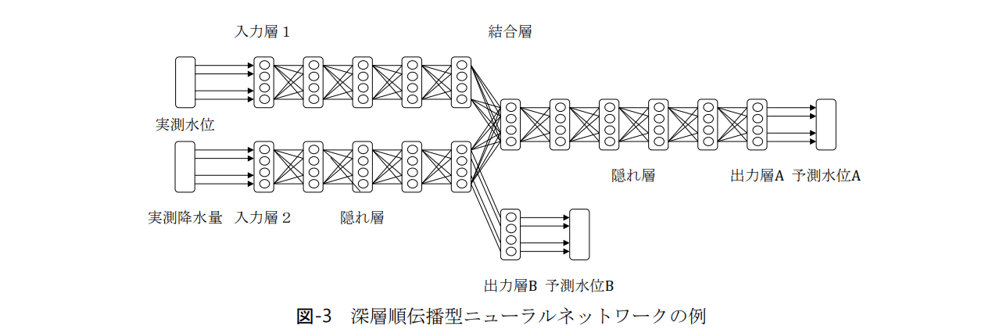
深層順伝播型ニューラルネットワークの模式図。出典:岡田治 他「AI による洪水予測と水位データの異常検知」平成 29 年度河川情報シンポジウム講演集 (2017)
順伝播型ニューラルネットワークは、予測値を計算する際に入力層から出力層へ向かって計算する(順方向)シンプルなニューラルネットワークの手法です。
浅層構造(隠れ層1層)のニューラルネットワークではピーク水位の予測精度が不十分であるため、流出モデルを組み合わせたり、隠れ層を増やすことで予測精度向上が試みられています。
動的(時間遅延)ニューラルネットワーク
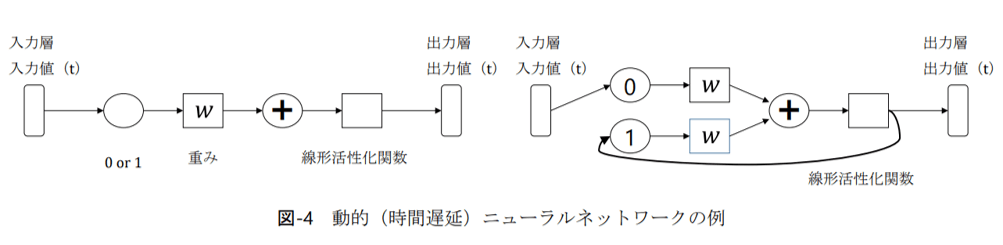
動的(時間遅延)ニューラルネットワークの模式図。出典:岡田治 他「AI による洪水予測と水位データの異常検知」平成 29 年度河川情報シンポジウム講演集 (2017)
動的(時間遅延)ニューラルネットワーク(TDNN; Time-Delay Neural Network)は、時系列データを入力とすることで時系列推移を考慮したアプローチです。
河川水位は時系列相関がある(上流の水位変化が時間差で下流に伝播)ため、時間幅をもたせたアプローチと相性が良いです。
LSTM
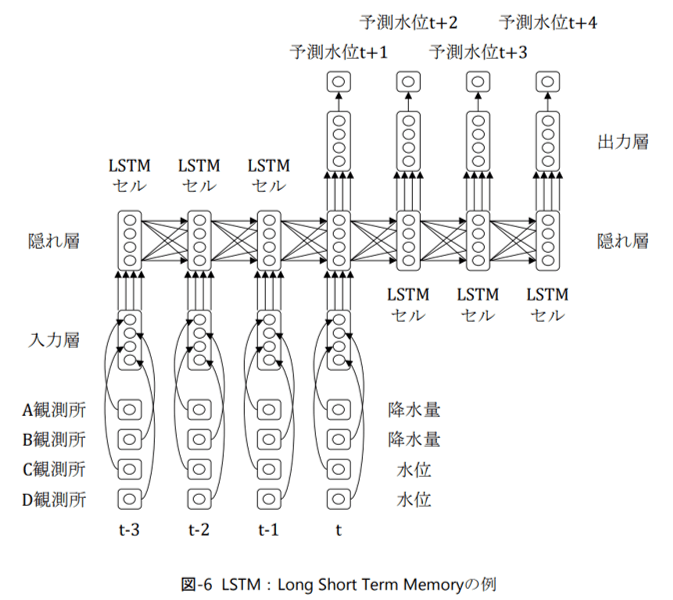
LSTMの模式図。出典:岡田治 他「AI による洪水予測と水位データの異常検知」平成 29 年度河川情報シンポジウム講演集 (2017)
LSTM (Long Short Term Memory) は再帰型ニューラルネットワーク(RNN; Recurrent Neural Network)の一種で、RNNの勾配消失問題の回避策として用いられます。
LSTMの前にその前提となるRNNについて説明します。
RNNは1つ前のデータの計算結果を次のデータの計算に使うニューラルネットワークで、時系列データに対して使われます。
時系列データは、直前のデータの値が直後のデータと相関があるという特徴をもつため、各時間の値は独立ではありません。
そのため、直前の計算結果を次の計算に利用するような内部ループ構造のロジックをもつRNNが使用されます。
最も単純なRNNであるSimpleRNNは、理論的には過去の計算結果を保持することができるはずですが、実際には勾配消失問題が発生するためうまくいきません。
RNNでは、出力層から入力層に向かって逆向きに誤差を計算し(誤差逆伝播法)、予測誤差が小さくなるように予測に使うパラメータの重みを調整します。
ニューラルネットワークの層が多数あると、出力層から入力層までを通したときに重みを改善できなくなり、学習ができなくなります(勾配消失問題)。
この問題を解決したのがLSTMです。
LSTMでは、前の時間の計算結果を次の計算に利用する際に、どの情報を次の計算に利用するかの重み付けを行います。
このLSTN層をはさむことで勾配消失問題を回避することができ、時系列データに対してRNNを適用できます。
参考文献
平岡透 他「Nearest-Neighbor法による河川水位予測の改良」土木学会論文集B 66(1) 99-103 (2010)
平岡透 他「降雨量からの河川水位予測の一手法」土木学会論文集B 66(1) 93-98 (2010)
藤原洋一 他「Neareast-Neighbor法による実時間流出予測の実用的適用法に関する研究」水文・水資源学会誌 16(1) 33-44 (2003)
【流出解析】シリーズ 第1回 流域界の決定と入力データの用意 Qiita 2022/12/17閲覧
中津川誠 監「Python による現場のための水文学」若手技術者水文学研究会(2022)
H-Q曲線 ウィキペディア 2022/12/17閲覧
用語集 国土交通省 四国地方整備局 2022/12/17閲覧
一言正之 他「深層学習を用いた河川水位予測手法の開発」土木学会論文集B1(水工学) 72(4) I_187-I_192 (2016)
岡田治 他「AI による洪水予測と水位データの異常検知」平成 29 年度河川情報シンポジウム講演集 (2017)
ニューラルネットワークの数学(順伝播) 株式会社キカガク 2022/12/21閲覧
Francois Chollet「Pythonによるディープラーニング」マイナビ出版 (2022)
Michael Nielsen「CHAPTER 5 ニューラルネットワークを訓練するのはなぜ難しいのか」 2022/12/23閲覧