データベースにおける正規化とは、整合性を保持しながら冗長なデータを分割して重複を削除する処理のことです。
1つの表にあらゆる情報を盛り込んでしまうと、本来同一であるべき情報が表の中で重複・分散して出現するため、データの更新や削除を行った際に、整合性を保つのが難しくなります。
データの更新・削除時に不整合・矛盾が発生しづらくするために情報を整理し、重複削除のために表を分割することが正規化の目的です。
正規化により1事実1箇所(1 fact 1 place)の状態を実現し、データの不整合(更新時異状)が起きることを抑制できます。
このページでは、正規化の段階について非正規形から第5正規形までを解説します。
正規化の段階
正規化にはいつくかの段階があり、段階を経るごとにデータの中の重複が減っていきます。
以下では、非正規形、第1正規形、第2正規形、第3正規形、ボイス・コッド正規形、第4正規形、第5正規形について順に解説します。
非正規形

非正規形とは、データの中に単一ではない属性が存在するデータのことです。
非正規形は正規化が一切なされていないデータであり、イメージとしては伝票や帳票をそのまま表に起こしたようなものです。
非正規形のデータは繰り返し項目(=単一ではない属性)が見られます。
繰り返し項目とは、エクセルで表形式で表示したときに一部の列のセルが結合されたようなデータであり、セル結合により視覚的にデータは見やすくなりますが、データベースにおいては扱いづらい形式です。
非正規形である例:属性Aが単一値でない(一部の属性に繰り返し項目が存在する)場合
第1正規形

第1正規形とは、データの全ての属性が単一値である(=非正規形ではない)データのことです。
非正規形の繰り返し項目を無くして、縦m行×横n行の単純な表形式にしたものです。
たとえば、エクセルにおいてセル結合を一切使わず、重複値は個別のセルに値を1つずつ入力したような表形式です。
第1正規形では、冗長なデータが含まれるため、整合性を保ちながら表を分割して第2正規形や第3正規形に変換していきます。
第1正規形である理由:全ての属性が単一値であり、候補キーの一部である属性Bに非キー属性Cが部分関数従属する場合
第2正規形

第2正規形とは、第1正規形の条件を満たし、かつ全ての非キー属性はいかなる候補キーにも部分従属していない(=完全関数従属である)データのことです。
候補キー:データの行を一意に識別できる属性(列)
主キー:候補キーのうち、実際にデータを一意に識別するために使用する属性(列)
非キー:候補キー以外の属性(列)
部分関数従属とは、候補キー(主キー)の一部(特定の列)の値が決まれば、同じ値になる列が存在している状態のことです。
特定の候補キーの列が同じ値の行では、部分関数従属している列はどの行でも同じ値になってしまいます。
そこで、候補キーの一部と部分関数従属している列を別の表に切り出すことで、重複を無くすことができます。
このように、候補キーの一部だけで値が決まってしまうような非キー属性(列)が一切存在しないデータを完全関数従属といいます。
第1正規形では冗長なデータが1つの表にまとまっていましたが、第2正規形では表を分割して部分関数従属を排除することで、データの重複を減らしています。
第2位正規形にすることで、データのトランザクション領域とマスタ領域を分離することができます。
このため、トランザクションとマスタを独立して更新(データの追加・変更・削除)を行うことができ、更新時異状を減らすことができます。
第2正規形である理由:全ての属性が単一値であり、候補キーからの部分関数従属が無く、推移的関数従属A→B→Cがある場合
第3正規形

第3正規形とは、第2正規形の条件を満たし、かつ全ての非キー属性はいかなる候補キーにも推移的関数従属していないデータのことです。
推移的関数従属とは、属性A, B, Cがあったとき、属性Aの値が決まれば属性Bの値が決まり、属性Bの値が決まれば属性Cの値が決まるというような推移的な関係が成り立つことをいいます。
ただし、属性Bから属性Aが決まる場合(属性AとBの立ち位置を入れ替えても成り立つ場合)は、推移的関数従属とは言いません。
第3正規形に直すことで、候補キー(属性A)から非キー属性(属性B)が決まった後に、さらにその非キー属性(属性B)から別の非キー属性(属性C)の値が決まってしまうという関係を無くすことができます。
また、候補キーの一部と非キー属性から別の非キーの値が一意に決まる場合も推移的関数従属であり、このような関係も第3正規形に直すことで無くすことができます。
第2正規形では候補キーに対する部分関数従属を無くしていましたが、第3正規形では推移的関数従属を排除することで非キー属性に起因する重複を削減できます。
こちらも、第1正規形→第2正規形の場合と同様に、更新時異状を減らすことができます。
第3正規形である理由:全ての属性が単一値であり、候補キーからの部分関数従属が無く、推移的関数従属も無い場合
ボイス・コッド正規形
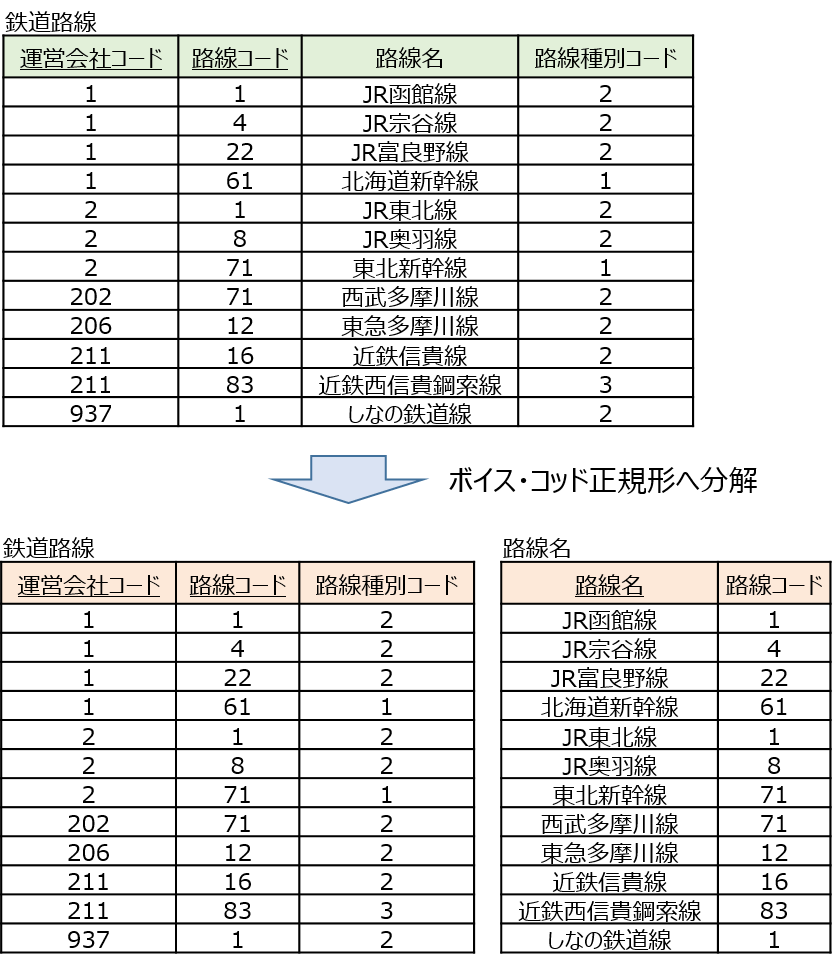
ボイス・コッド正規形とは、候補キー以外の非キー属性の値によって別の属性の値が決まってしまうような関係を排除したデータのことです。
候補キー:データの行を一意に識別できる属性(列)の組み合わせのうち極小のもの(=データを一意に識別するために不要な属性(列)を一切含まない組み合わせ)
スーパーキー:データの行を一意に識別できる属性の組み合わせ全て(データを一意に識別するために不要な属性が入っていても良い)
定義としては、データにおけるあらゆる関数従属X→Yにおいて、①X→Yが自明な関数従属であるまたは②Xはスーパーキーであることのいずれかが成り立つことです。
①における自明な関数従属とは、X→YにおいてYがXの部分集合にあたる状態のことです。
この際、X→Yは常に成立します。
第3正規形が成立する場合においても、非キー属性から主キーの一部が決まってしまう関係が残ることがあり、この場合はボイス・コッド正規形ではありません。
一方、主キーが1つしかない場合は、主キー属性単独で主キーである(=スーパーキーでもある)ため必ず②成立し、第3正規形であれば必ずボイス・コッド正規形となります。
第3正規形までは情報無損失分解(=表を自然結合すると分解前の表を復元できる)ですが、ボイス・コッド正規形への表分割は情報無損失分解ではありません。
このため、表分割によりボイス・コッド正規形にすることで一部の関数従属が失われ、元データには存在しないような関係のデータを追加できてしまいます。
このため、実務的には第3正規形までの分解にとどめ、整合性制約を課すことでデータの一貫性を保持します。
ボイス・コッド正規形である理由:全ての属性が単一値であり、全ての関数従属が自明であるか候補キーのみを決定項として与えられている場合
第4正規形

第4正規形とは、ボイス・コッド正規形の条件を満たし、かつ自明でない多値従属を含まないデータのことです。
多値従属とは、1つの属性の値が決まれば、別の属性Yの値が1つ以上決まる性質のことです。
たとえば、従属性IDが決まれば、その従業員が保有する資格(複数の場合あり)が決まるといった性質です。
「自明でない」多値従属とは、互いに独立した意味を持つ複数の多値従属が存在することです。
たとえば、従業員IDが決まれば、従業員の担当顧客と保有資格がそれぞれ決まるといった関係です。
ボイス・コッド正規形まで正規化すると多くの場合では第4正規形も満たしますが、非キー属性が存在せず候補キーが複合キーである場合には、自明でない多値従属が含まれて第4正規形を満たさない場合もあります。
第4正規形の定義としては、データにおけるあらゆる多値従属X→→Yにおいて、①X→→Yが自明な多値従属であるまたは②Xはスーパーキーであることのいずれかが成り立つことです。
第4正規形である理由:全ての属性が単一値で、全ての多値従属が自明であるか、候補キーのみを決定項として与えられている
第5正規形

第5正規形とは、ボイス・コッド正規形の条件を満たし、かつ自明でない結合従属を含まないデータのことです。
結合従属とは、1つの属性の値が決まれば、別の属性Yの値が1つ以上決まる性質のことです。
結合従属性は関係従属や多値従属を包含する概念です。
関数従属の場合はこのような関係性が1つしかなく分解できない場合であり、多値従属の場合はこのような関係が2つのテーブルに分解できる場合を指します。
3つ以上のテーブルに分解できる場合は結合従属です。
「自明でない」結合従属とは、互いに独立した意味を持つ複数の結合従属が存在し、3つ以上のテーブルに分解できる場合です(2つに分解できる場合は多値従属)。
たとえば、小売店のレシート番号がわかれば、
第5正規形の定義としては、データにおけるあらゆる結合従属*(A1, A2, …, An)において、①*(A1, A2, …, An)が自明な結合従属であるまたは②Ai(i=1,…, n) はスーパーキーであることのいずれかが成り立つことです。
第5正規形である理由:全ての属性が単一値で、全ての結合従属性が自明であるか、候補キーのみを決定稿として与えられている
参考文献
三好 康之「情報処理教科書 データベーススペシャリスト」翔泳社(2025)