ゲーム理論は元々経済学の一分野でしたが、現在では学問の枠を飛び越えて様々な分野に応用されています。
このページでは、ゲーム理論を公共交通機関の不正乗車対策に応用した例について解説します。
信用乗車方式における特別改札

ベルリンのSバーンの鉄道駅に設置されている乗車券の打刻機(ドイツ)。信用乗車方式の鉄道路線では、事前購入した乗車券を使う場合には駅に設置している打刻機で日時を打刻してから乗車する。特別改札(抜き打ち検札)時に打刻されていない乗車券を持っている場合は不正乗車として扱われる。出典:Wikimedia Commons, ©Nicolas Bouliane, CC BY-SA 4.0, 2023/9/24閲覧
鉄道やバスなどの公共交通機関では、正確な運賃の収受が大きな課題となっています。
欧米の都市部の公共交通機関では、駅で改札を行わない代わりに抜き打ちで検札(特別改札)を行い、適正なきっぷを所持していない場合は問答無用で高額なペナルティを課す信用乗車方式が採用されています。
信用乗車方式では駅で改札を行わないため、無賃乗車による収入減少を防ぐための特別改札が鍵となります。
特別改札を行う際には、「限られた人員で徴収する金額を最大化すること」と「検札担当者の動きが乗客に予測されないこと」の2点が重要になります。
検札を行う人員を増やすほど徴収できる金額は増加しますが、検札担当者一人あたりが徴収できる金額は減っていきます。
検札担当者には人件費がかかるため、その人数は人件費と徴収できる金額のバランスを見て最適化する必要があります。
さらに、同じ人員で徴収できる金額を最大化するために、検札を行う時間帯やルートを工夫する必要があります。
時間帯や路線、駅によって不正乗車を行う人数は変わるため、徴収金額を最大化できるルートの特定は重要です。
検札担当者が定期的に同じルートばかりを回っていると、そのルート上では不正乗車が減って徴収金額が減る一方で特別改札を行わない場所・時間帯で不正乗車が増加します。
そのため、検札担当者のルートや時間帯が乗客に予測されない必要があります。
以上のような特別改札の課題を解決するための方法として、ゲーム理論を用いた手法が試みられています。
以下では、ゲーム理論の特別改札ルート最適化への応用の第一歩として「限られた人員で徴収する金額を最大化」できるようなモデルについて解説します。
シュタッケルベルグ競争モデルを用いた特別改札ルート最適化
信用乗車方式における特別改札(抜き打ち検札)ルートを最適化するために、シュタッケルベルグ競争モデルによる最適化が試みられています。
シュタッケルベルグ競争はゲーム理論のモデルの1つであり、プレイヤーをリーダーとフォロワーに分けて、リーダー→フォロワーの順番に意思決定を行う完備情報の動学ゲームです。
特別改札ルート最適化では、検札チームをリーダー、乗客をフォロワーとみなします。
乗客のうち一定数は金銭的に自分が得をする選択をすると考えられます。
つまり、特別改札チームに遭遇する機会が少なければきっぷを購入せず、特別改札チームに遭遇する機会が多ければきっぷを購入するということです。
そのため、特別改札チームの動きに応じて、特別改札チームが回らない時間・場所では不正乗車が増加し、反対に集中的に特別改札を行う場所・時間では不正乗車が減少します。
このような現象をシュタッケルベルグ競争として数式でモデル化する試みが行われています。
特別改札ルートのモデル化
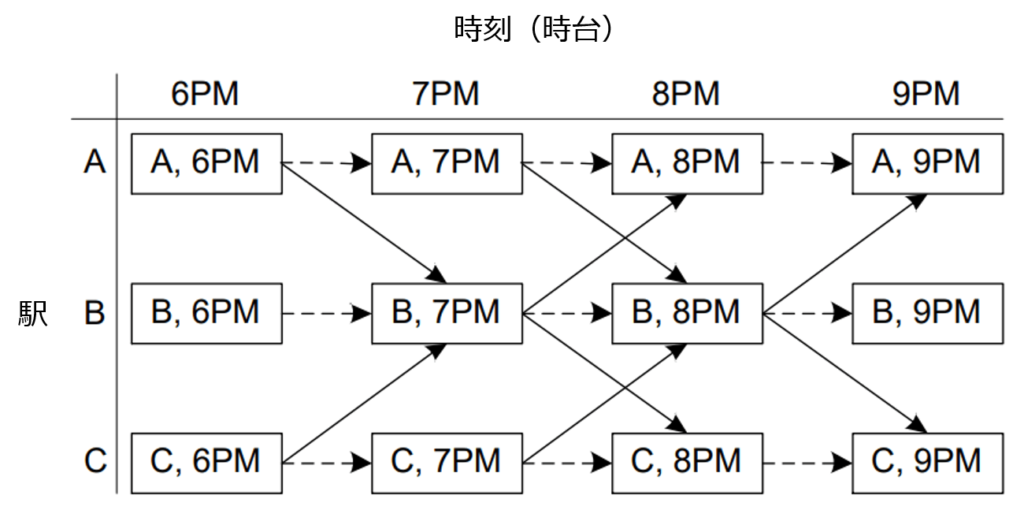
特別改札(臨時検札)チームの巡回ルートの模式図。3つの駅A, B, Cがある1本の路線について1時間単位での巡回ルートの選択肢をネットワーク(グラフ)として表現している。たとえば、午後7時(7PM)にB駅に滞在(改札実施)している場合、午後8時台には次の3つの選択がある。①A駅に移動しして改札を実施する。②引き続きB駅に滞在して改札を実施する。③C駅に移動して改札を実施する。このような選択の連続をネットワークとして表現することで最適なルートを数値計算で解を求めることができる。このネットワーク(グラフ)の最適化問題を解くことで、徴収できるペナルティ運賃を最大化できるルートを求めることができる。出典:Z. Yin et al., TRUSTS: Scheduling Randomized Patrols for Fare Inspection in Transit Systems, Proc. Innov. Appl. Artif. Intell. Conf. 26(2) (2012) Figure 2
特別改札ルートを数式でモデル化するためには、巡回ルートの場所と時間をシンプルに表現する必要があります。
上の図は、特別改札チームの移動ルートをネットワーク(グラフ)として表現したものです。
ここでは、3つの駅A, B, Cからなる1本の鉄道路線を考えます。
1つの頂点はある時間に特定の駅での滞在(特別改札実施)に対応しています。
簡略化のために時間は1時間単位で1つの頂点で表しており、頂点間の枝(エッジ)は時間の推移(同じ駅へ引き続き滞在 or 別の駅へ移動)を表します。
たとえば、午後7時(7PM)にB駅に滞在(特別改札実施)している場合、午後8時台には次の3つの選択があります。
①A駅に移動しして改札を実施
②引き続きB駅に滞在して改札を実施
③C駅に移動して改札を実施
このような選択を繰り返すことで特別改札チームのルートを決めることができます。
さらに、各時間・場所での特別改札による収入の期待値の分布がわかると、巡回ルートごとの収入を算出できます。
ネットワーク上のルートは無数に設定できますが、現実の巡回には様々な制約があります。
特別改札担当者も労働者であるため、早朝から深夜まで巡回し続けることは出来ませんし、途中の休憩時間も必要です。
このため、実際にルートを決める際には種々の制約条件を数式で表現して最適化問題に落とし込む必要があります。
実用を考えると、決められた線区の範囲内でおおむね8時間分の巡回ルート(昼休憩1時間を含む)を設定するといった形が想定されます。
このような制約条件を満たす巡回ルートは無数にあり、運賃徴収効率が悪いルートから良いルートまで様々なルートがあります。
そこで、過去の特別改札の記録や不正乗車比率の調査結果を元に、運賃徴収効率が良いルートを選択していく運用が想定されます。
不正乗車比率の調査事例
モデル化を行うためには過去の各時間・場所での不正乗車比率のデータが必要です。
次の2つの地図は、サンフランシスコの公共交通機関において、不正乗車比率を調べてマッピングしたものです(上:ルート別、下:調査地点別)。
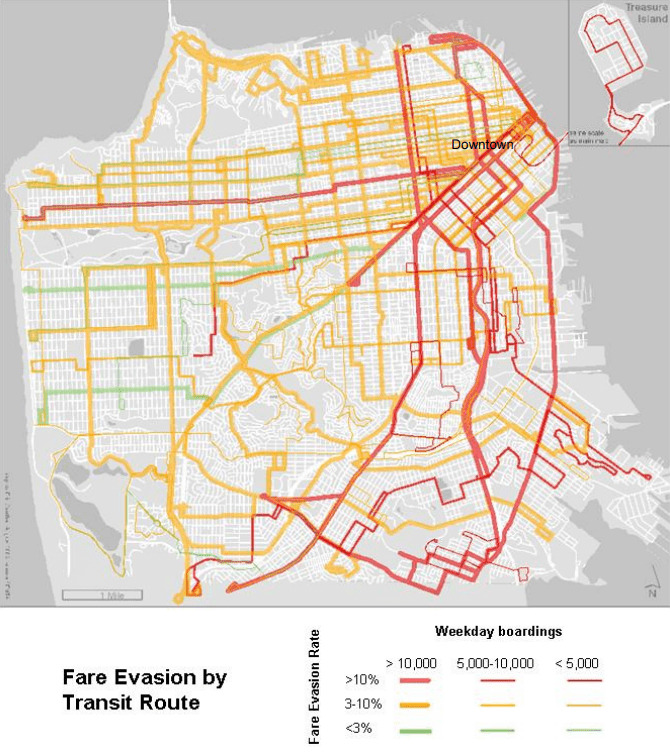
公共交通機関のルート別の平日の乗客数と不正乗車比率(米国カリフォルニア州サンフランシスコ市)。線が太いほど乗客数が多く、緑 (<3%)、オレンジ (3-10%)、赤 (<10%) の順に不正乗車比率が高い。出典:J. Lee, Uncovering San Francisco Muni’s Proof-of-Payment Patterns to Help Reduce Fare Evasion, Transp. Res. Rec. 2216(1) p75-84 (2011)(全文)

公共交通機関の調査地点別の平日の乗客数と不正乗車比率(米国カリフォルニア州サンフランシスコ市)。円が大きいほど乗客数が多く、緑 (<3%)、オレンジ (3-10%)、赤 (<10%) の順に不正乗車比率が高い。出典:J. Lee, Uncovering San Francisco Muni’s Proof-of-Payment Patterns to Help Reduce Fare Evasion, Transp. Res. Rec. 2216(1) p75-84 (2011)(全文)
上の地図を見ると、北東部のダウンタウン周辺で乗客数が多い上に不正乗車の比率が高くなっています。
他には、ダウンタウンから南方向に乗客数と不正乗車比率が高い場所が伸びています。
一方で南西部方面の路線は乗客数も少なく不正乗車比率も比較的低いです。
以上より、ダウンタウン周辺とダウンタウンから南に伸びる幹線路線で特別改札を行うのが効率が良さそうです。
このような路線・地点ごとの不正乗車比率のデータを元に、ある駅にある時間帯に特別改札を行った場合の収入(例:A駅に午前7時台に特別改札を実施した場合に1,000ドル徴収)を算出できます。
シュタッケルベルグ競争モデルでは、ネットワーク上の頂点(特別改札を行う駅と時間帯の組み合わせ)ごとの収入がわかるため、収入を最大化できるネットワーク上のルート(特別改札ルート)を数値計算で算出できます。
以上のように、ゲーム理論を応用することで特別改札ルートを最適化して収入を最大化する試みが行われています。
参考文献
L. Brotcorne et al., Fare inspection patrols scheduling in transit systems using a Stackelberg game approach, Transp. Res. B: Methodol. 154 p1-20 (2021)(全文)
Z. Yin et al., TRUSTS: Scheduling Randomized Patrols for Fare Inspection in Transit Systems, Proc. Innov. Appl. Artif. Intell. Conf. 26(2) (2012)
J. Lee, Uncovering San Francisco Muni’s Proof-of-Payment Patterns to Help Reduce Fare Evasion, Transp. Res. Rec. 2216(1) p75-84 (2011)(全文)
L. Dauby and Z. Kovacs, Fare Evasion in Light Rail Systems, Transp. Res. Circ. p230-247 (2007)(全文)